 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
The first step to measuring the size of the universe is to find the distance to the planets within our own solar system. We can break that task down into several steps.
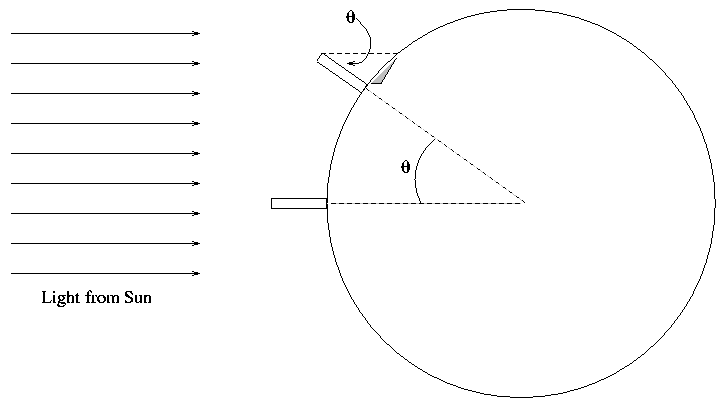
Eratosthenes heard that, one one particular day during the summer, the sun was directly overhead at noon in the city of Syene. He went out on that day and measured the angle of a shadow cast at noon in his own town of Alexandria. The angle theta of that shadow is equal to the angle theta between the two cities, as seen from the center of the Earth:

This angle told him the fraction of the Earth's circumference which must lie between Syene and Alexandria -- it turned out to be about 1/50. So the distance between Syene and Alexandria (which could be measured by pacing or using a cart with a calibrated wheel) had to be about 1/50 of the circumference of the entire Earth. He calculated that the Earth had a circumference of about 25,000 miles, and thus a radius of about 4,000 miles. He was very close to the right value!
Strangely enough, people didn't pay attention to Eratosthenes' value as well as they should have. The influential astronomer Ptolemy adopted a smaller value in his treatise Almagest, and many followed Ptolemy's lead. One of them was Christopher Columbus, a mariner in search of riches and fame. He wanted to find a route from Europe to the Orient by sea (to cut out all the middlemen in the lucrative spice trade). Was it possible? Most people said, "No way -- it's too far for a ship to travel," but Columbus made two crucial assumptions:
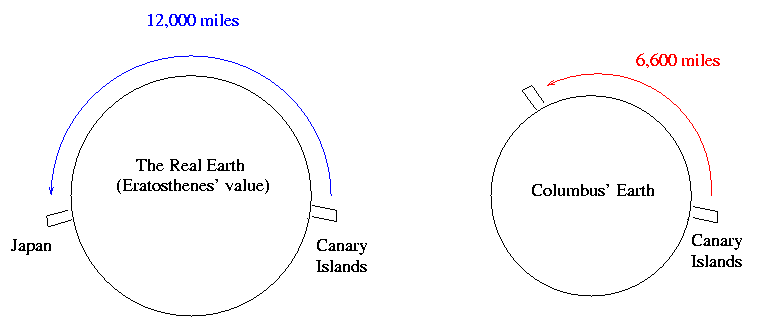
The distances shown in this figure take into account Columbus' plan to decrease the distance he had to travel by sailing at a latitude of 30 degrees North.
The net result of these two big errors was that Columbus underestimated the true distance he would have to travel by almost a factor of two! It was no wonder that Columbus had trouble finding a sponsor for his mission: any competent geographer would assure his patron that a sea voyage to China was doomed to end in death for the sailors. And, indeed, if Columbus hadn't accidently run into the Americas, he and his crew would have died of thirst and starvation.
In order to calculate the distance to the Moon, or Jupiter, or the nearby stars, one must use a technique called trigonometric parallax. It is based on geometry.
There are special mathematical tools one can use to determine the lengths of the sides of a right triangle. In the figure below, suppose that we want to know the distance L.
If we can measure the side B, and the angle alpha, then we can use the equation
B
L = ----------
tan(alpha)
to calculate L.
We can use the same method for a situation in which there are two such triangles, back-to-back:
We can still figure out the distance L with trigonometry. Once again, we calculate
B
L = ----------
tan(alpha)
but we could also describe this as
1/2 (2B)
L = --------------------
tan [ 1/2 (2*alpha) ]
or
half of the total baseline
L = ----------------------------
tan [ half the total angle ]
In most astronomical applications, the distance L is much, much longer than the baseline B, and the angle theta is much, much less than one degree. In such situations, the simpler formula
the total baseline
L = ----------------------------
tan [ the total angle ]
gives an answer which is identical to the more complicated
(but formally correct) formula.
It's easy to measure the parallax of the Moon, without any optical aid. As long as two observers are separated by several thousand miles, they will see the Moon appear in obviously different positions relative to nearby stars.
Below is a picture showing a view of the Moon and stars from Rochester, New York, on Wednesday, Jan 17, 2001, at 5:00:00 AM EST. The picture is 20 degrees across. If you click on the picture, you will be shown the same area of the sky, at the same time, as seen by an observer in Lima, Peru. By clicking repeatedly on the image, you can "blink" the two views. Watch how the Moon shifts its position by about its own diameter.
The shift is even more obvious if one zooms in closer. Here's a view of the same situation with binoculars, showing a field 5 degrees across:
If one knows the size of the Earth, and hence the distance between Rochester and Lima, one can calculate the distance between the Earth and the Moon, based on this shift.
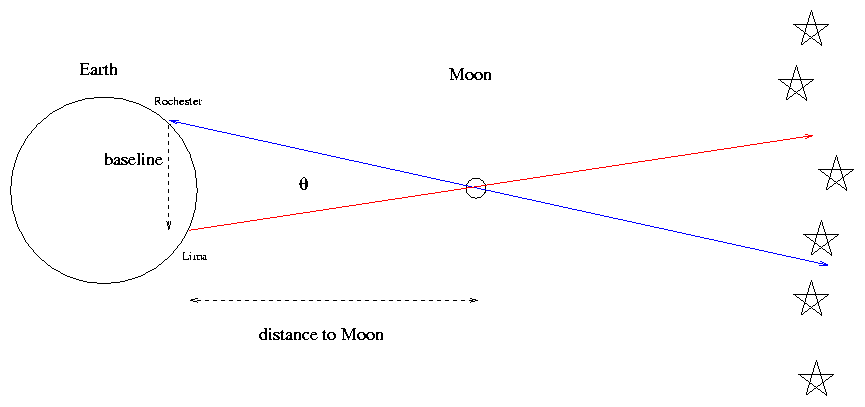
(Note that this figure is not to scale!)
For some reason, none of the ancient Greek astronomers used this simple method of parallax to measure the distance to the Moon. Certainly it was difficult to travel long distances, but there were thriving communities in the Mediterranean basin over a thousand miles apart. Arranging to make simultaneous observations would have been difficult in a world without clocks, but again, not impossible.
The Greek astronomers did manage to use geometry to measure the distance from the Earth to the Moon; they just chose slightly more complicated methods.
In fact, the shift is invisible to the naked eye. One must use a telescope and make very careful measurements in order to detect the shift of Mars against the background of stars. The picture below shows a close-up, telescopic view of Mars and a few stars. It has a field of view of only 0.13 degrees. Click on the picture to blink views from the two cities.
The picture above shows Mars and a number of nearby stars which might be used as references. It looks as if it would be a simple matter to measure the position of Mars relative to these reference stars. In real life, there's a big problem: Mars is very bright -- much, much brighter than the great majority of stars which close enough to it to serve as references. That makes it very difficult to measure Mars' position accurately.
Are there any other bodies in the solar system which are better suited to parallax measurements than Mars? Yes -- in two very different situations.
Here's a photograph of the transit of Venus in 1882, taken from Wellington, South Africa.

The basic idea is that observers at different points on the Earth will see Venus silhouetted in front of different points on the Sun:

(Note that this figure is not to scale!)
Throughout the eighteenth and nineteenth centuries, the European powers used their navies as transports for astronomers: scientific expeditions to far-flung corners of the globe spent years travelling in order to observe transits. Captain Cook's final expedition (during which he was killed on the Hawaiian islands) was part of an English research program to observe the transit of Venus in 1769. Cook, astronomer Charles Green, and botanist Daniel Solander successfully observed the transit from Tahiti on June 3, 1769.
Again, the basic idea is to observe the asteroid from widely separated locations on Earth, and measure the shift in its apparent position with respect to background stars.
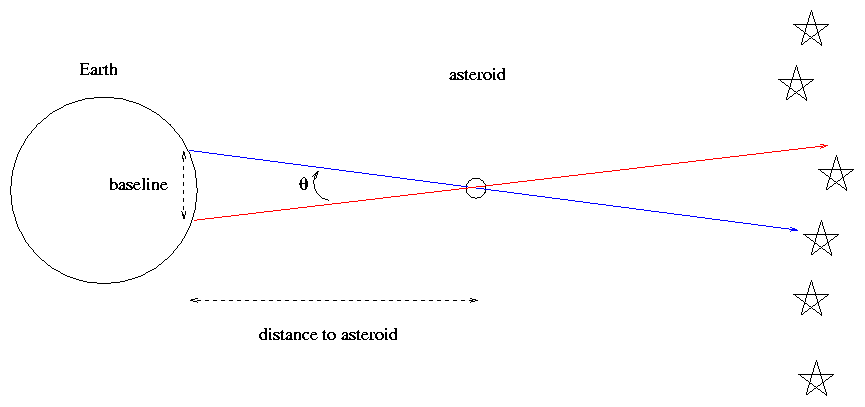
(Note that this figure is not to scale!)
The closer the asteroid comes to the Earth, the larger the parallax and the easier it is to measure. In 1931, the asteroid Eros came within 16 million kilometers of the Earth (compared to mininum distances of 42 million km for Venus and 55 million km for Mars). Observatories around the world measured its position very carefully over a period of several months, and -- many years later -- the data were finally reduced to yield
Is it necessary to measure directly the parallax to every single body in the solar system -- Eros, and Venus, and Mars, and Jupiter, etc.? The answer is No, thank goodness, because we can make accurate measurements for only a very few of these bodies. But as soon as we have one good distance, we can use it to determine all the distances.
The reason goes back to the German astronomer Johannes Kepler. Kepler used the visual measurements of Tycho Brahe to figure out several rules governing the motions of planets:
2 3
(period) = K * (radius)
where the constant K is the same for all planets
in the Solar System.
Kepler's Third Law is the crucial one in this case. The period of an orbit is easy to measure -- all it takes is time and patience. One can simply watch the motion of a planet (say, Jupiter) relative to the stars. Right now (January, 2001), Jupiter is close to the star Aldebaran. If one watches closely, one can see that Jupiter appears to move eastward, relative to Aldebaran. By July, 2001, Jupiter will have moved about twenty degrees away from Aldebaran. After about twelve years, Jupiter will have moved all the way around the sky (relative to the stars) and appear close to Aldebaran again. If one is willing to keep track over several revolutions, one can determine the period of any planet to high precision.
Over the centuries, scientists measured the periods of all the major planets (including the Earth's) very accurately. They knew, for example, that the period of Earth was 365.24 days, and the period of Mars was 687 days. Kepler's Third Law allows one to calculate the relative sizes of the orbits of the Earth and Mars:
2 2
(Earth's period) (Mars' period)
----------------------- = K = ------------------------
3 3
(Earth's orbital radius) (Mars' orbital radius)
and therefore
2 3
(Earth's period) (Earth's orbital radius)
------------------ = ----------------------------
2 3
(Mars' period) (Mars' orbital radius)
and therefore
2/3
( Mars' period )
Mars' orbital radius = (Earth's orbital radius) * ( -------------- )
( Earth's period )
2/3
( 687 days )
Mars' orbital radius = (Earth's orbital radius) * ( -------------- )
( 365.25 days )
= 1.52 * (Earth's orbital radius)
Astronomers knew all the relative sizes of the orbits -- but they didn't know the absolute sizes. If they could measure the absolute size of any single orbit, they could then use that to calculate the absolute sizes of all the orbits.
The first really good result came from measurements of the parallaxes to several asteroids in the late 1880s. These measurements told us the absolute distance (in meters) between the Earth and the asteroids. We already knew the relative sizes of the orbits. A little algebra allows one to combine these pieces of information and derive the absolute size of the Earth's orbital radius, and therefore the absolute sizes of all the planets' orbits.
For more information:
 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.