Assignment 4: Simulate a Microlensing Event

Due Monday, Apr 3, at 1:00 PM.

Your job this week is to work out an example of a microlensing event in our galaxy.

Preliminary Trig Factoid

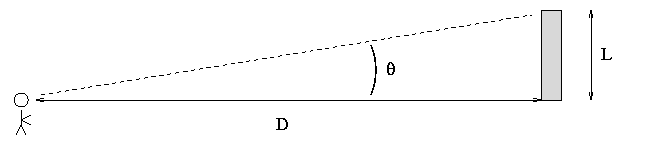
You will need to use this handy fact of mathematical life: if an object of length L is seen from a very large distance D,

then its angular size measured in radians is

        theta = L / D

One can also turn this around: if you know the angular size of an object in radians and its distance, you can figure out its size:

        L  =  D * theta

The situation

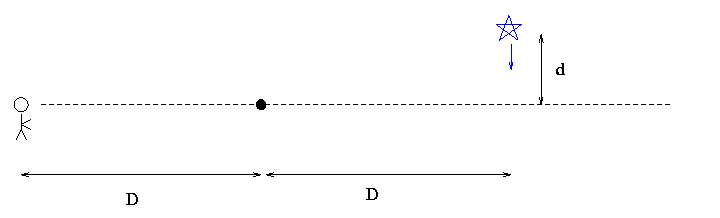
We look towards the bulge of the Milky Way, which is about 10 kiloparcsecs away from us. Halfway there, at a distance of D = 5 kpc, there is a star identical to our Sun; it acts as a gravitational lens. Call this star the "lensing star". Beyond the lensing star, another D = 5 kpc away, is a very bright star which will act as the background source. Call this star the "background star." The background star is, today, March 29, 2000, off to one side of the lens by a distance d = 2.0 x 10^12 meters.

Looking at the situation from far above it all:

Now, the background star won't pass directly in back of the lens, but it will come close. It is moving with a speed of v = 100 km/sec relative to the lens, and at closest approach will come within b = 2.5 x 10^(-9) radians of the lens:

Looking at the lens from the Earth:

Questions

What is the radius of the lensing star (which is identical to the Sun)?
What is the mass of the lensing star?
What is the angular size of the lensing star, in radians?
What is the Einstein ring radius of the lensing star, in radians?
Which is larger, the angular size of the lensing star or its Einstein ring radius?
What is the current angular distance between the background star and the lensing star, in radians?
Does the background star pass within the Einstein ring radius of the lens? What is the ratio of its closest approach to the Einstein ring radius?
How long will it take for the background star to move from its current position to its point of closest approach to the lens?
On what date will that occur?

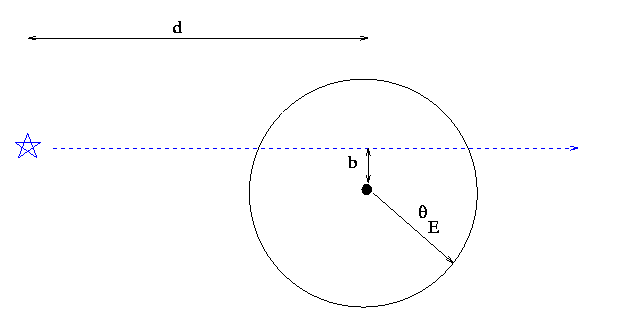
Now, for the gravitational lensing: how much brighter does the background star become? Well, if from our point of view, the angular distance between the background star and the lens is r radians, then the amplification factor due to lensing is

  Let   u  =  r/theta_E

  Then
                           u^2 + 2
        amplification = -----------------
                        u * sqrt[u^2 + 4]

You might use the Pythagorean theorem to calculate the angular distance r from the angular distance to the side of the lens at some time and the angular distance of closest approach, b.

Lensing questions

What is the maximum amplification factor for this event?
On what date does the maximum amplification occur?
Make a table which shows the amplification factor at intervals of 50 days, starting today (March 29, 2000), and ending after 400 days.
Make a graph which shows the amplification factor on the y-axis, and time (in days since today) on the x-axis.

Last modified by MWR, Mar 29.5, 2000