 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
So, there Big Bang model explains several observed features of the universe. But it contains a number of parameters -- knobs and buttons, you might consider them -- which control the precise behavior of the universe as it expands. Some of the most important of these are:
Check out the cast of characters for a summary of these and the major players in the Big Bang theory.
We need to figure out the values of these parameters in order to predict the past (and future) evolution of the universe.
In order to measure the Hubble Constant -- the rate at which the universe is currently expanding -- one must measure
The Hubble Constant is then simply the ratio of the two:
radial velocity km/sec
H = ------------------ ------
distance Mpc
One complication is that the velocities of some galaxies are modified by gravitational forces from other galaxies. For example, a galaxy in a cluster may have a peculiar velocity of up to 1,000 km/sec, positive or negative, due to its motion within the cluster. If the "natural" radial velocity of a galaxy would be only 2,000 km/sec, its motion within a cluster could modify its apparent radial velocity greatly.
In order to make accurate measurements of H, it helps to look at very distant galaxies, because their radial velocities are so large -- say, 20,000 km/sec -- that gravitationally-induced peculiar velocities are negligible. Unfortunately, it is very difficult to measure distances to such galaxies. It's a bit of a catch-22:
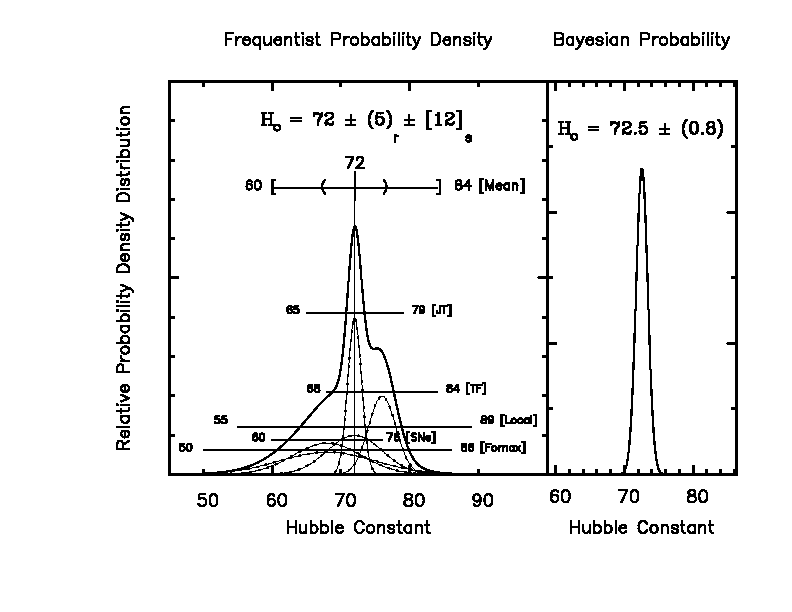
The best current estimates for the Hubble Constant are somewhere around
H = 60 - 80 km/sec/Mpc

What does the value of H imply?
If H is large the universe is expanding age since the
rapidly, so it didn't starting point
take long to reach its is "small"
current size
If H is small the universe is expanding age since the
slowly, so it has taken starting point
a long time to reach its is "large"
current size
In fact, to a very rough approximation, the value of H gives the age of the universe; just figure out its numerical value after cancelling all the units you can, and then take the reciprocal.
km/sec m / sec 1
H = ------ = -------- = -----
Mpc m sec
1
--- = sec
H
Now, this isn't the true age of the universe, just a rough approximation that may be accurate to within a factor of two or so. Why isn't it the true age? Because it assumes that the universe has been expanding at the current rate ever since the starting point. But that's not true, because gravitational forces have been slowing down the expansion ... so the true age depends on how much matter there is in the universe.
And, if the cosmological constant is not zero, it has also been changing the expansion rate, causing it to increase.
Is there any way to check this age estimate? Yes. One way to is use the known rates at which radioactive elements decay:

In the star, they found lines of uranium (the parent element) and thorium (the daughter element). Notice just how tricky it is to measure the strength of the uranium line!
Based on their measurements, they determine an age of 12.5 +/- 3 billion years.
The more matter there is, the more its gravitational force opposes the expansion of the universe. If there is enough matter, more than the critical density, then the universe may eventually stop expanding and begin to contract.
How can we measure the amount of matter in the universe? There are several ways:
Typical values for visible matter density is
visible matter density = 0.001 to 0.01 * (critical density)
dark matter density = 0.05 to 0.2 * (critical density)
It turns out that the relative amounts of these light elements depends very sensitively on the density of the universe during those early times. The higher the density, the larger the amount of helium produced, and the smaller the amount of deuterium (because the deuterium fuses into helium more easily when density is high).
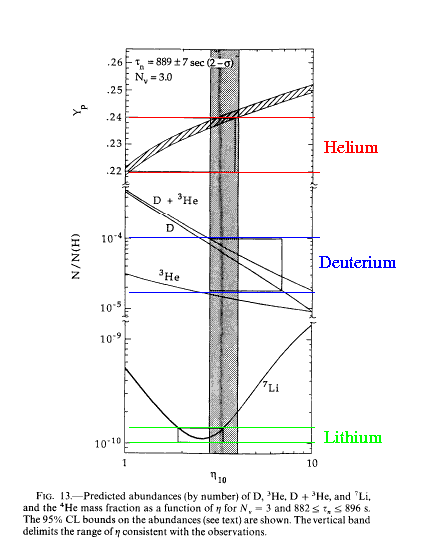
Our best measurements of the abundances of these light elements lead us to conclude that the density of baryonic matter (ordinary matter, which makes up the ordinary elements) is
baryonic matter density = 0.015 to 0.05 * (critical density)
No matter how you slice it, it appears that the amount of matter (visible, dark, or baryonic) is far below the critical amount needed to halt the expansion of the universe. So, if the only factor in the evolution of the universe was the gravitational attraction of matter, the universe would never stop expanding....
The behavior of space is governed by the theory of general relativity (GR). GR describes space as (possibly) being "curved". What does that mean?
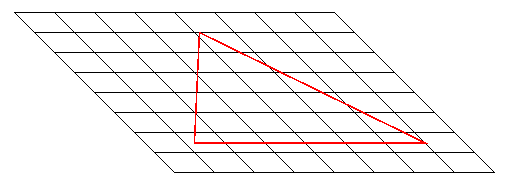
Consider an analogy to our three-dimensional universe: a two-dimensional world, a Flatland upon which creatures wriggle. If the creatures have taken high-school geometry, they can test their 2-D universe for curvature by drawing a triangle and measuring the angles. In a Euclidean, flat space, the angles will add up to exactly 180 degrees:
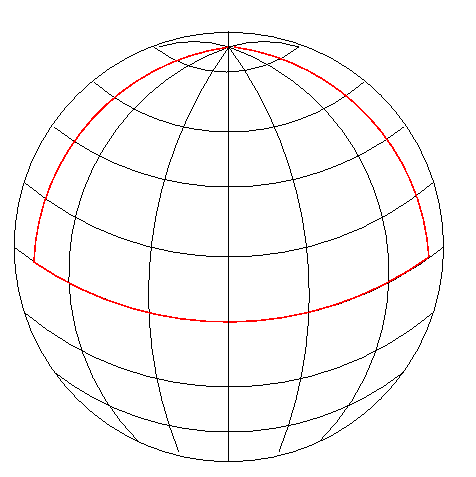
But if the creatures happen to live on a sphere, a positively curved space, they will notice that the sum of the angles of a triangle is more than 180 degrees:
Drawing big triangles isn't the only way to test for curvature. Some other tests are:
There are three possibilities for the geometry of a 3-D universe
curvature angles brightness size
--------------------------------------------------------------
flat sum = 180 dims as the shrinks as the
inverse square inverse of
of distance distance
positive sum > 180 dims more slowly shrinks more
(sphere) than inverse slowly than
square the inverse
negative sum < 180 dims more quickly shrinks more
(saddle) than inverse quickly than
square the inverse
Solutions to Einstein's equations of general relativity indicate that a completely empty universe would have negative curvature, and would expand rapidly and forever.
But GR also indicates that space can be "warped" by the presence of matter. Matter has two effects on the space in its vicinity:
When Einstein solved the equations of general relativity, he found that there was another factor, besides matter, which might "warp" space. He called this factor the cosmological constant, usually denoted by the capital Greek letter lambda. Now, the cosmological constant is wierd:
but
So, is there any evidence for a non-zero cosmological constant? Yes -- but it's a bit indirect. The evidence goes something like this:
If we believe we know the true luminosity of Type Ia supernovae, and we can observe them at great enough distances, we might be able to check for any deviation from the linear relationship -- which would indicate the overall curvature of the universe.
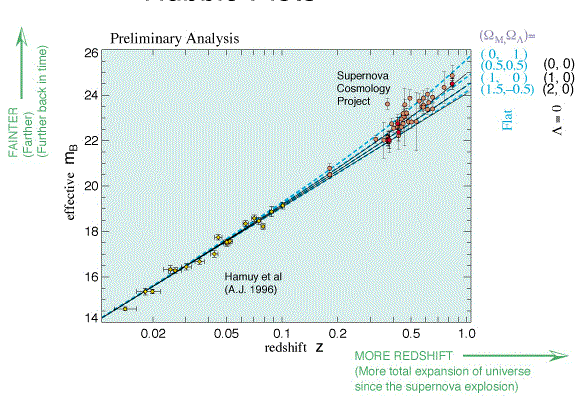
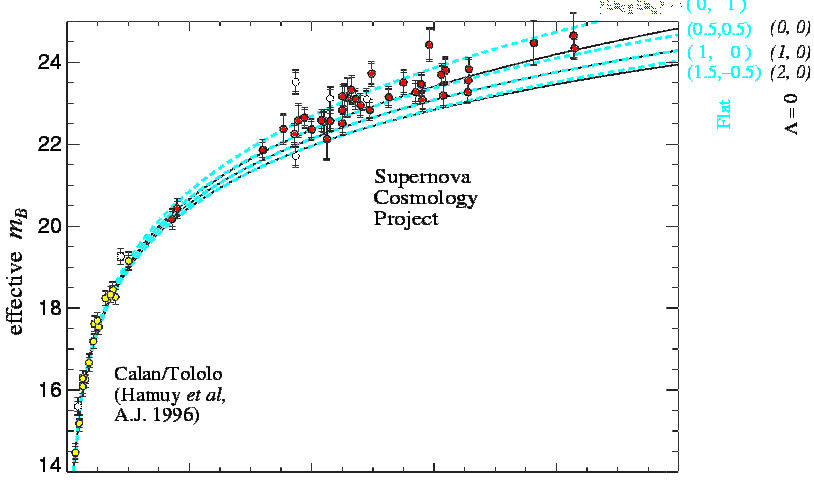
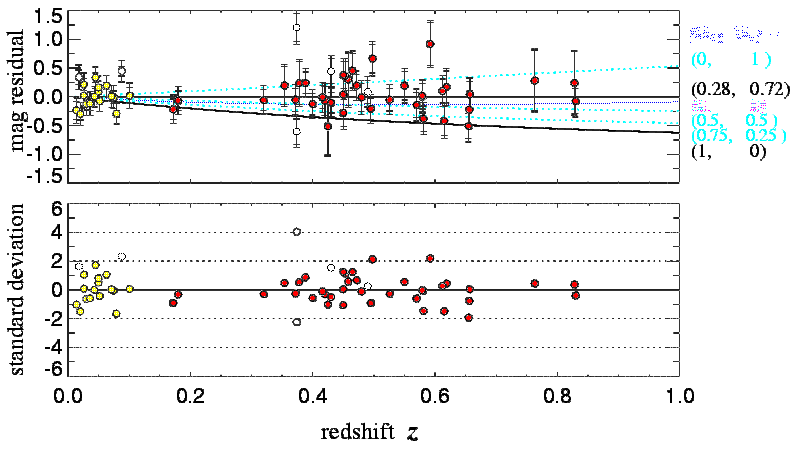
The current observations indicate that there is probably some negative curvature to space; and, if given the very small matter density, this indicates a relatively large value for the cosmological constant. The basic result from the supernova observations is that the cosmological constant is probably between 0.5 and 1.0.
and in simulations of the universe:

These "clumps" are clusters of galaxies, and groups of clusters, and concentrations of groups of clusters, and so on. Because material at the center of clump exerts a strong gravitational pull on its surroundings, it attracts nearby material, and grows with time. A big clump at the current time must have been a smaller clump at an earlier time.
In fact, we can run simulations of the universe, in which we take the current distribution of galaxies and follow them backwards in time. The big, obvious clusters and superclusters turn into smaller, very subtle blobs in the early universe. Our simulations tells us how big those blobs ought to be when the universe became neutral and transparent for the first time.
If we compare the actual size of the blobs in the microwave background with the size predicted by simulations, we can check for the curvature of space:
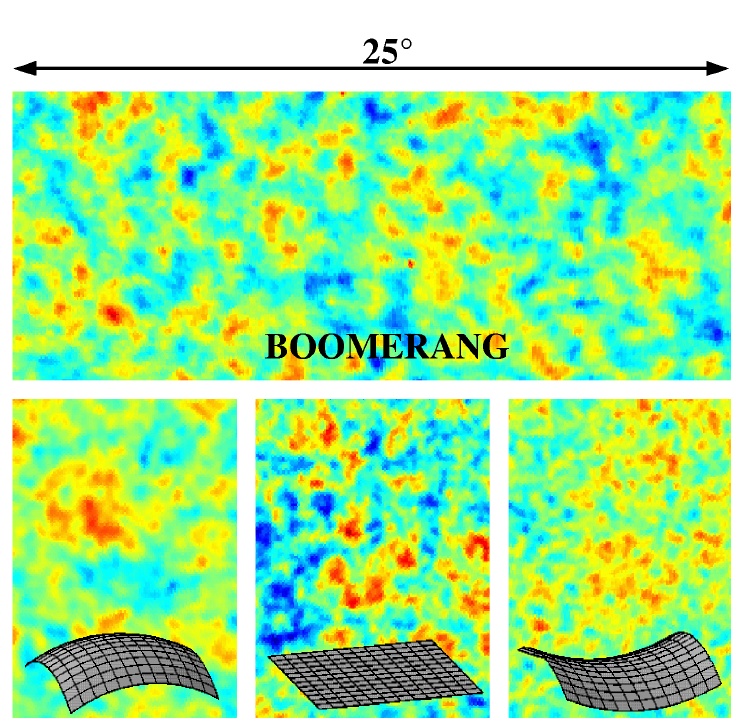
The size of the blobs in the BOOMERANG maps are pretty darn close to what we'd expect if the universe is geometrically flat. Again, since we can estimate how much curvature is caused by the relatively small matter density, we can figure out how much of the remainder must be due to the cosmological constant. The basic result from BOOMERANG is that the cosmological constant is probably between 0.5 and 1.0.
Another balloon-borne experiment to measure the CMB, called MAXIMA, has reached a similar conclusion. It looked at a somewhat smaller area of the sky (and in a different direction), but with higher resolution. The maps made by the two experiments are very similar. The pictures below show a square roughly 10 degrees on a side from BOOMERANG on the left, MAXIMA on the right:

If we combine information from the supernova observations and the CMB observations, we can place reasonably strong constraints on two important cosmological parameters:
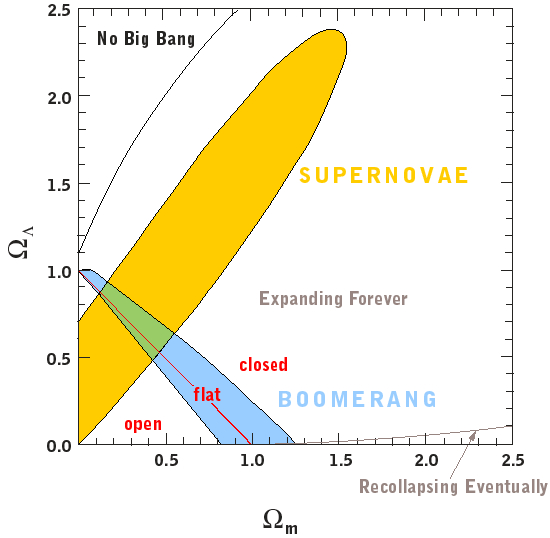
At the present time (Feb 13, 2001), it looks like the matter density is only about 30 percent of the critical density (with only 5 percent or so due to ordinary baryonic matter). Because the overall geometry of the universe appears to be flat, that means that the cosmological constant must contribute about 70 percent of the critical density.
For more information,
 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.