Distances via Parallax

Knowing the distance to a star or planet is necessary to determine several of its properties (size, mass, density, luminosity) ... but is also difficult to measure. Celestial objects are inaccessible: we can't visit them ourselves, or (in the case of stars and galaxies) even send robotic vehicles to them. Therefore, astronomers have devised a number of schemes to measure distances indirectly. You will use the best of them tonight: the parallax method.

Parallax

If one looks at the same nearby object from different locations, it will appear to shift side-to-side relative to more distant objects. You can see the effect yourself by holding one arm out in front of you, pointing at some feature on a distant wall. Raise one finger on the hand. Close your left eye, and note the position of your finger relative to the wall. Then open your left eye, and close your right eye: your finger will appear to have moved relative to features on the wall.

Planets and stars are too far away to show shifts as you shift from one eye to the other ... but they do display apparent motion if you use longer baselines. One possibility is to arrange for two observers far apart on the Earth -- say, Rochester and San Francisco -- to observe an object simultaneously: a baseline of several thousand miles permits them to see a shift in the apparent position of asteroids and planets relative to the stars. Another technique is to make observations of a star six months apart, as the Earth moves from one side of the Sun to the other in its orbit: this baseline of almost two hundred million miles will reveal small shifts in the apparent positions of nearby stars relative to more distant ones.

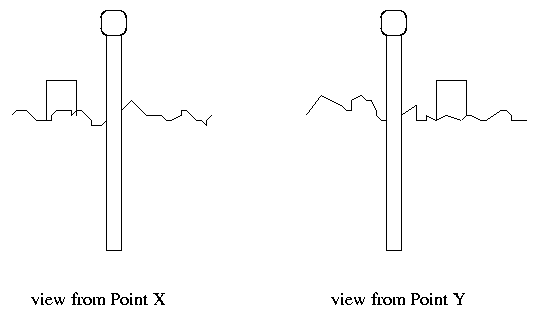
Your task to is measure the distance to a streetlight in the parking lot in front of the Center for Imaging Sciences by parallax. I have marked two spots for you to stand: point X is close to the building, and point Y is a distance 8.5 meters away on the sidewalk. From each spot, you should be able to see the streetlight and, behind it, one of the skyscrapers in downtown Rochester.

You must measure the angular shift of the streetlight relative to the distant skyscraper: that is, assume the building's direction is fixed, and measure the total angular motion, in degrees, by which the streetlight appears to move. You will have a simple device with which to measure angles: a meter stick with a centimeter scale on a cross-piece attached to one end.

Draw a bird's-eye view of the CIS building, locations X and Y, the streetlight, and the direction towards the skyscraper.
Record your raw measurements with the measuring device: how many centimeters apart are the streetlight and skyscraper, as seen from point X? From point Y?
Turn the raw measurements into angular measurements: how many degrees apart are the streetlight and skyscraper from point X? From point Y?
What is the total angular motion of the streetlight relative to the skyscraper, in degrees? We call this the parallax of the streetlight.
Using your bird's-eye diagram, your determination of the parallax, and some trigonometry, determine the distance to the streetlight.

Last modified Sep 20, 2001 by MWR