 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Knowing the distance to a star or planet is necessary to determine several of its properties (size, mass, density, luminosity) ... but is also difficult to measure. Celestial objects are inaccessible: we can't visit them ourselves, or (in the case of stars and galaxies) even send robotic vehicles to them. Therefore, astronomers have devised a number of schemes to measure distances indirectly. You will use two of them tonight: parallax and the inverse square law.
If one looks at the same nearby object from different locations, it will appear to shift side-to-side relative to more distant objects. You can see the effect yourself by holding one arm out in front of you, pointing at some feature on a distant wall. Raise one finger on the hand. Close your left eye, and note the position of your finger relative to the wall. Then open your left eye, and close your right eye: your finger will appear to have moved relative to features on the wall.
Planets and stars are too far away to show shifts as you shift from one eye to the other ... but they do display apparent motion if you use longer baselines. One possibility is to arrange for two observers far apart on the Earth -- say, Rochester and San Francisco -- to observe an object simultaneously: a baseline of several thousand miles permits them to see a shift in the apparent position of asteroids and planets relative to the stars. Another technique is to make observations of a star six months apart, as the Earth moves from one side of the Sun to the other in its orbit: this baseline of almost two hundred million miles will reveal small shifts in the apparent positions of nearby stars relative to more distant ones.
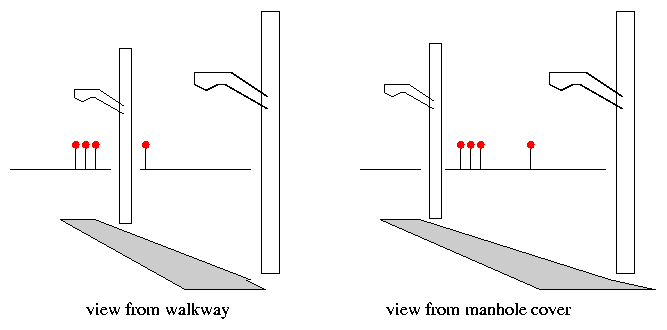
Your task to is measure the distance to a streetlight in the parking lot in front of the Center for Imaging Sciences by parallax. I have marked two spots for you to stand: point A is close to the building, and point B is a distance 7 meters away on the sidewalk. From each spot, you should be able to see the streetlight and, behind it, one of the skyscrapers in downtown Rochester.
You must measure the angular shift of the streetlight relative to the distant skyscraper: that is, assume the building's direction is fixed, and measure the total angular motion, in degrees, by which the streetlight appears to move. You will have a simple device with which to measure angles: a meter stick with a centimeter scale on a cross-piece attached to one end.
If two identical lights are placed at different distances from an observer, he will notice a difference in their brightness: the nearby one will appear brighter, and the distant one dimmer. If he measures their brightnesses carefully, he will find that they obey the inverse square law:
2
intensity of object 1 ( distance to object 2 )
------------------------- = ( -------------------- )
intensity of object 2 ( distance to object 1 )
Astronomers sometimes use this law to estimate distances: if we believe that two stars are identical, and we know the distance to one of them, we can use their apparent intensities to determine the distance to the other. Of course, we never really know that the two are identical in their intrinsic luminosity, so this is always just an educated guess. In addition, if the one known distance has any uncertainty, then the derived distance will have an even larger uncertainty. Overall, this method is not a truly reliable one -- but it is sometimes the best we can do.
You will use this method to make a second estimate of the distance to the streetlight observed in the Parallax section (call it "Light 1"). Here's how: there is another streetlight (call it "Light 2"), much closer to the Center for Imaging Sciences. You may measure the distance between Point B and Light 2 directly, by pacing it. Assume that the two streetlights shine with identical luminosity. If you can measure the relative brightness of the two lights, you can use the inverse square law to calculate the distance to Light 1.
You may borrow a set of neutral density filters from the instructor. Each set consists of 6 small squares of plastic material. This material is manufactured so that a single layer of it will block half of the light incident on it; the other half is transmitted: If you look through 2 layers of it, then the first layer blocks half the incident light, and the second blocks half of what's left; thus, only one-quarter of the incident light passes through.
brightness of Light 2
-----------------------
brightness of Light 1
distance to Light 2
-------------------
distance to Light 1
Do the two different methods yield the same distance? Each involves some approximation, of course: so "reasonable agreement" might mean "the same to within 20% or so." If the two disagree by more than 20%, try to explain why. Which method do you think is more accurate in this experiment, and why?
Last modified Sep 22, 1999 by MWR
 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.