Measure the Earth's Radius with a Stopwatch

Is it possible to measure the earth's radius -- armed only with a stopwatch? Yes! The answer will be only approximate, but that's a lot better than nothing.

The basic idea is to look at a sunrise or sunset (or moonrise or moonset) in a very particular manner:

For a sunrise (or moonrise)
1. Stand and face the eastern horizon.
2. As soon as you see the top limb of the Sun (or Moon) appear above the horizon, start the stopwatch.
3. Lie down, quickly.
4. Continue to watch the eastern horizon. The Sun (or Moon) should -- for a brief time -- have disappeared below the horizon.
5. As soon as the Sun (or Moon) appears again, stop the stopwatch.
For a sunset (or moonset)
1. Lie down and face the western horizon.
2. As soon as you see the top limb of the Sun (or Moon) disappear below the horizon, start the stopwatch.
3. Stand up, quickly.
4. Continue to watch the western horizon. The Sun (or Moon) should -- for a brief time -- have reappeared above the horizon.
5. As soon as the Sun (or Moon) disappears again, stop the stopwatch.

The time it takes for the Sun (or Moon) to re-appear (or re-disappear) is related to the angle through which the Earth has rotated between (dis)appearances. If you can measure the time accurately, you can calculate the angle accurately. Use the following proportion:

    time between disappearances       angle through which Earth rotates
    ---------------------------   =   ---------------------------------
         one entire day                         360 degrees

Okay, now what -- how can knowing the angle by which the Earth rotates help you to calculate the Earth's radius? Consider the following. Big Sam and Little Sam stand side-by-side to watch a sunrise. Big Sam is six feet tall, Little Sam is only three feet tall. Which one sees the sun first? Click on the figure below to find out...

Big Sam will see the Sun rise first, because his head will peek above the Earth's shadow first. Little Sam will have to wait for the Earth to rotate a bit farther in order for his head to rise above the shadow.

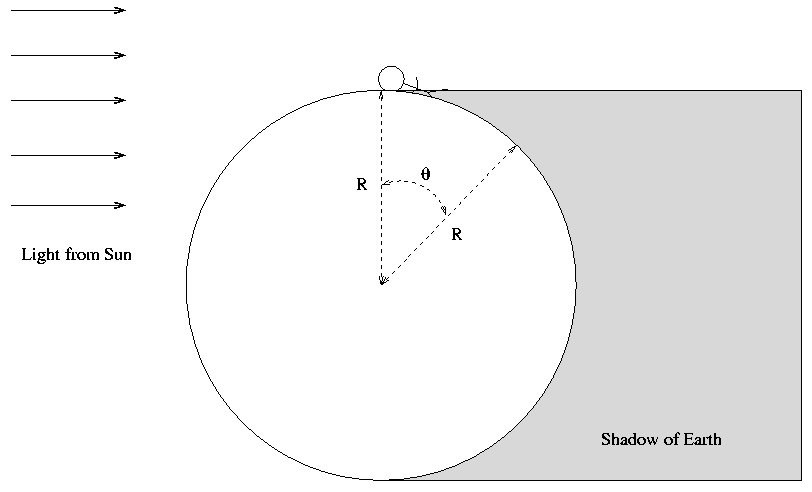
Exactly the same effect occurs when you watch a sunrise: there will be one particular moment when you are standing and just able to see light from the Sun.

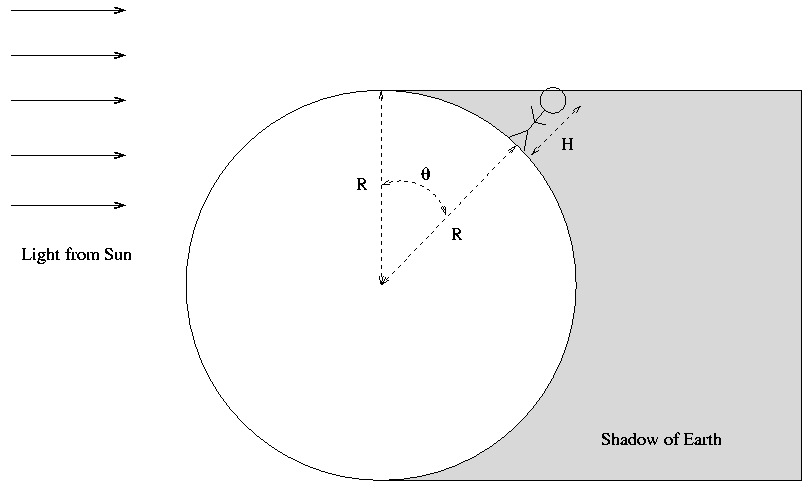
If you quickly lie down, so that your head is effectively at ground level, then the Earth will have to rotate an extra amount to bring you into the light:

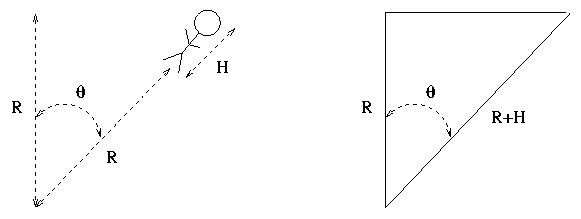
If you know that angle theta, and you know your height H, you can use a little trigonometry to calculate the radius of the Earth R.

Try it! If you have the opportunity, do this experiment several times on different occasions. How well do the results agree?

Will the answer you get depend on your latitude? All the diagrams I've drawn show the observers on the equator. Does it matter?

I welcome reports from anyone who has carried out this experiment. Please send your results to mwrsps@rit.edu and I'll include them in a later version of this page.

Added Dec, 2015

tanushree did the experiment and reports the following:

       Height                165 cm
       Time to re-appear      10 seconds
       Calculated radius    6200 km

Other ways to measure the size of the Earth

If you live near the San Franciso Bay, you can perform a most scenic experiment involving the Golden Gate Bridge, as described by Karl Hahn.

Last modified by Michael Richmond on Dec 23, 2015.