 Viewgraph 1
Viewgraph 1
 Viewgraph 2
Viewgraph 2
 Viewgraph 3
Viewgraph 3
 Viewgraph 4
Viewgraph 4
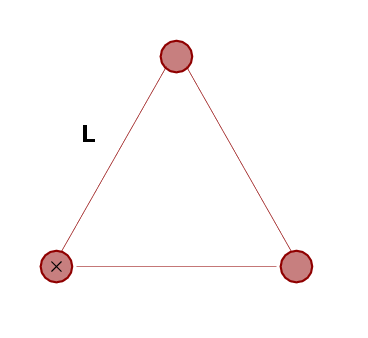
Let's try an easy calculation: what's the moment of inertia of these three balls? Each ball has mass m = 3 kg, and they are arranged in an equilateral triangle with sides of length L = 10 m. We spin the triangle around the spot marked "X", which is one of the balls.
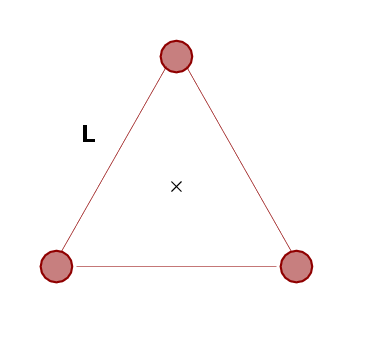
Okay, let's try a harder one. Suppose that we locate the center of mass of the triangle -- I've marked it with the "X" in the figure below. What's the moment of inertia of the triangle spun around this point?
 Viewgraph 4
Viewgraph 4
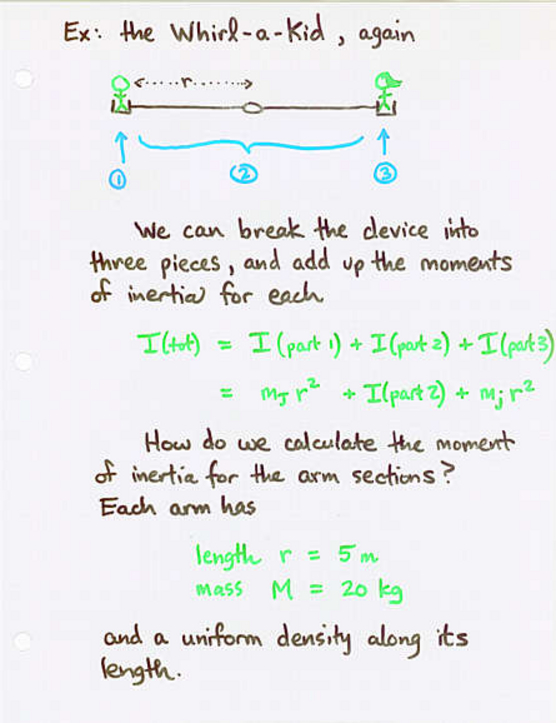 Viewgraph 5
Viewgraph 5
 Viewgraph 6
Viewgraph 6
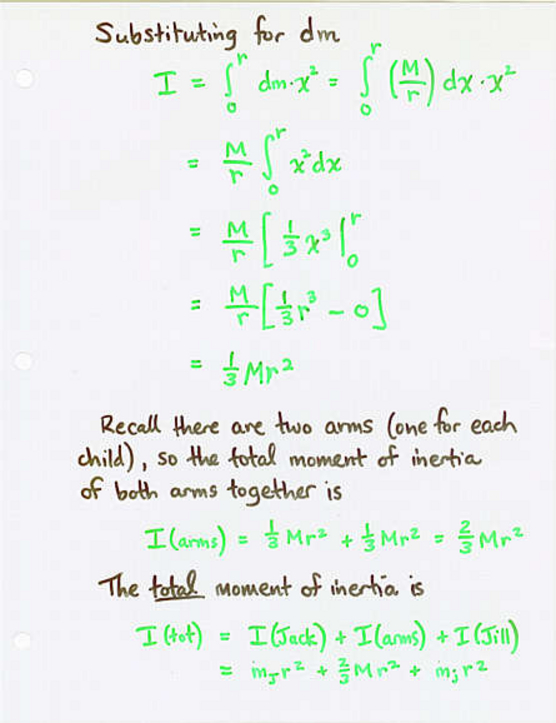 Viewgraph 7
Viewgraph 7
 Viewgraph 8
Viewgraph 8
 Viewgraph 9
Viewgraph 9 Viewgraph 10
Viewgraph 10