Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
On August 20, 1977, NASA launched the Voyager 2 spacecraft for a mission to the four giant planets of the solar system: Jupiter, Saturn, Uranus and Neptune.
Image courtesy of
JPL and NASA
After the probe separated from its booster rockets and sped away from Earth's orbit, it had a speed (relative to the Sun) of about v0 = 38,500 m/s.
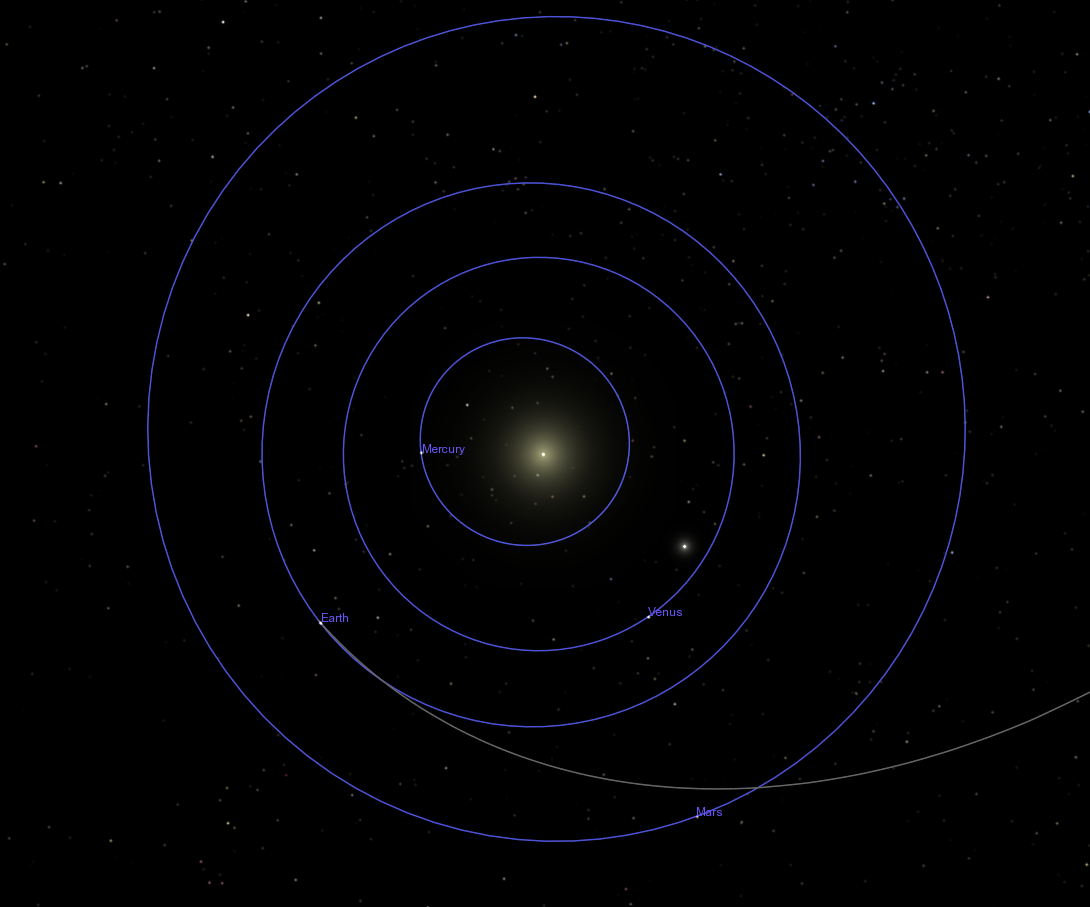
Q: Given an initial distance from the Sun
R = 1.0 AU = 1.496 x 1011 m
and an initial speed relative to the Sun of
v0 = 38,500 m/s
what is the maximum distance Voyager 2 could
travel away from Sun? Express your answer in AU.
Q: Is that far enough to reach its targets?
Jupiter 5.2 AU
Saturn 9.5 AU
Uranus 19.2 AU
Neptune 30.1 AU
No! Voyager 2's initial speed would allow it to reach Jupiter, but none of the other giant planets. What were the rocket scientists thinking?
What they were thinking was that they were very lucky. The year 1977 was a very fortunate time to be sending space probes to the outer planets. Take a look at the positions of the giant planets at the time of launch:
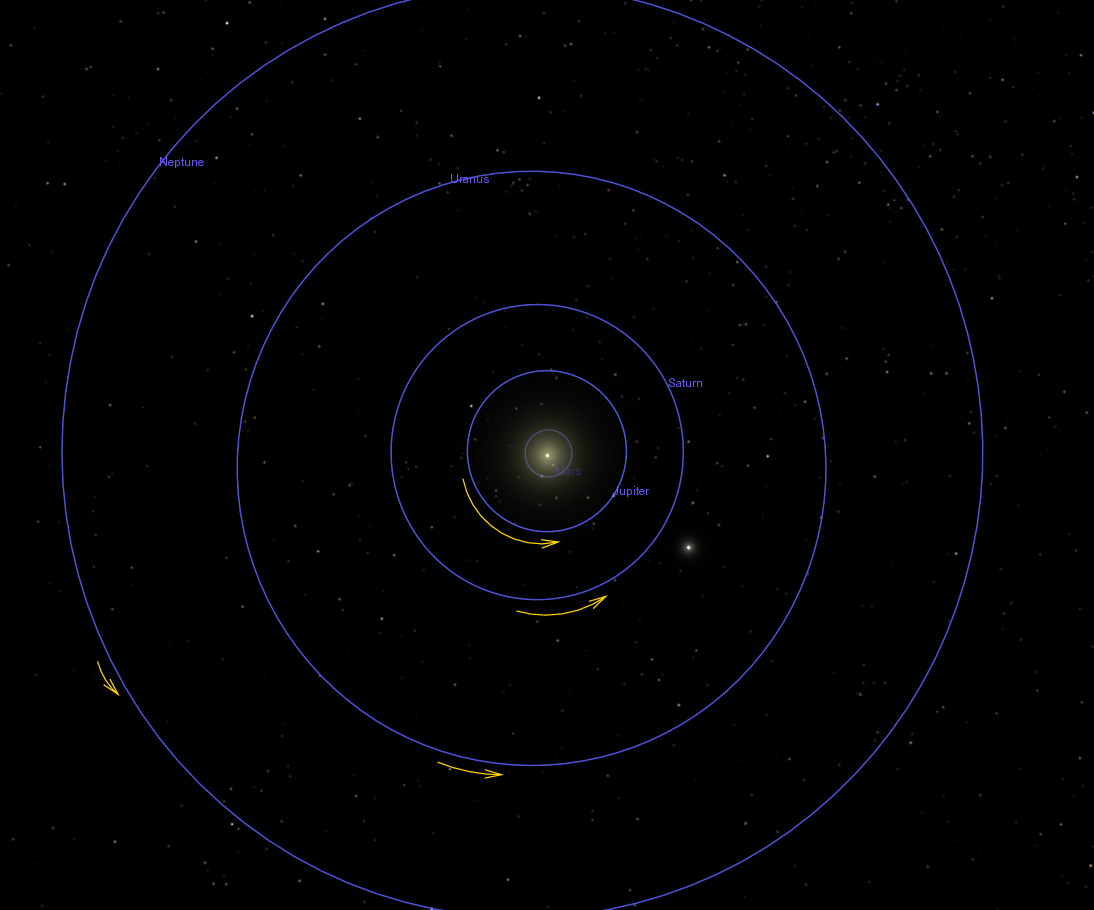
The planets are all moving counter-clockwise in this view, seen from far above the plane of the solar system. As you can see, Neptune is ahead of Uranus in its orbit, and Uranus is ahead of Saturn, and Saturn is ahead of Jupiter.
If there were some way for each planet to give the spacecraft a "push" forward during its visit, then
Jupiter could push it forward to Saturn ... Saturn could push it forward to Uranus ... Uranus could push it forward to Neptune ...
But how could this work? And would each "push" be strong enough to give Voyager the boost it would need?
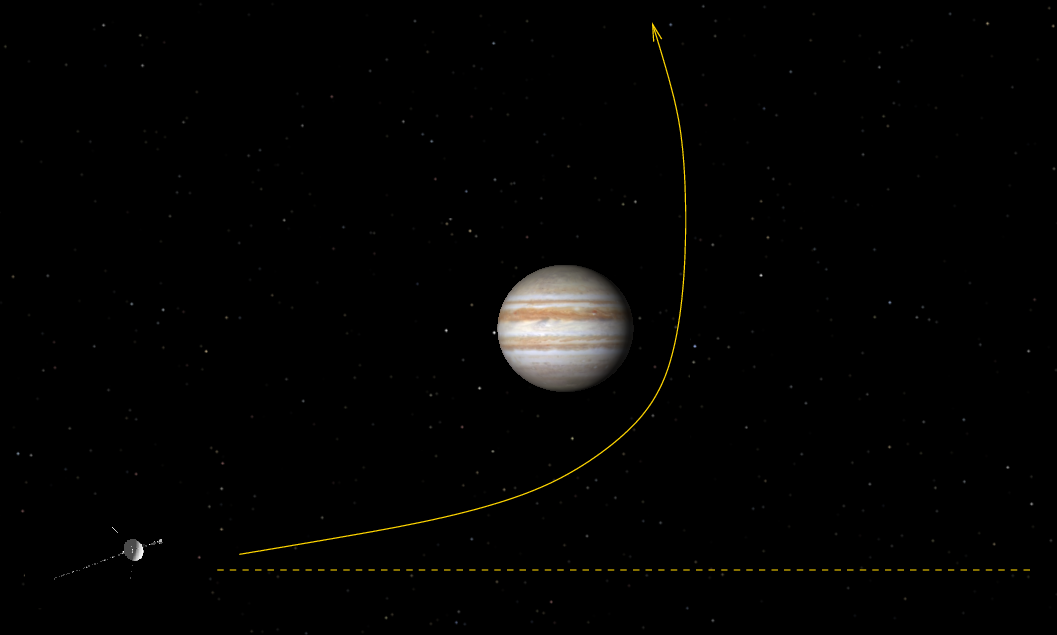
Suppose that a spacecraft flies past a planet:
At every moment, the two objects exert gravitational forces on each other. The forces are equal in size, and oriented toward the center of each object.
When the objects are close together, the forces grow larger ...
... and as they separate, the forces decrease.
The effect of these forces is to change the momentum of each object by the same amount, but in opposite directions. Of course, since the spacecraft's mass is small, this impulse causes its velocity to change by a very significant amount, modifying its trajectory. The planet's velocity changes by a very, very, very small amount ... but definitely not by zero!
As long as the spacecraft remains sufficiently far from the planet's atmosphere and surface, there is no friction, nor any resistance forces. The interaction is therefore elastic, which means that both momentum and kinetic energy are conserved.
Depending on the initial positions and velocities of the planet and spacecraft, the exchange of momentum -- and hence the change in trajectories -- could be small, or quite large:
In order to simplify things, we can consider the entire interaction to consist of three stages.
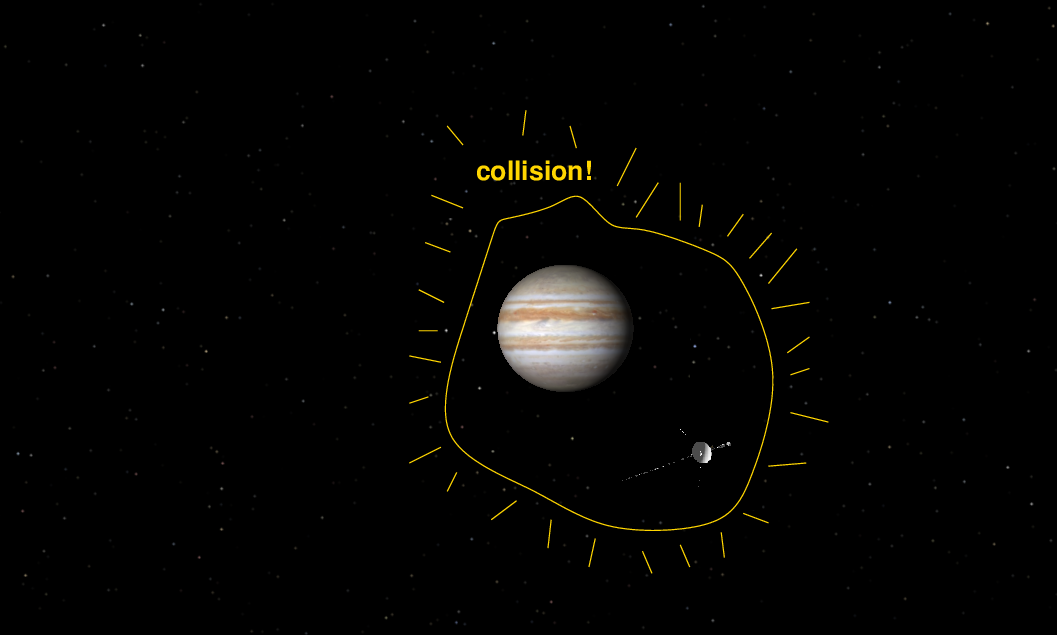
So, let's go back to a very simplified version of this actual situation. Suppose that we have a very big ball of big mass M which is moving through space with initial velocity v. It runs into a very small ball of mass m << M , which is -- for further simplicity -- sitting motionless.
To make things EVEN simpler, let's assume that the collision is exactly head-on, so that afterwards, both objects continue to move in the same direction as the initial velocity.
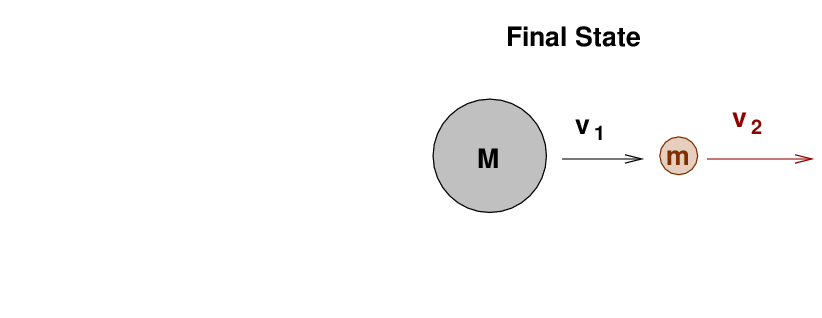
In this elastic collision, just as in the gravitational interaction between Jupiter and Voyager, both energy and momentum are conserved. That means that if we know the initial information
M = mass of the big object
m = mass of the small object
v = initial velocity of the big object
then we ought to be able to figure out the speeds of the two objects after the collision:
v1 = final velocity of big object
v2 = final velocity of small object
After all, we have two equations connecting these two unknown quantitiies.
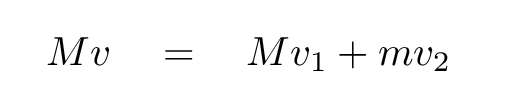
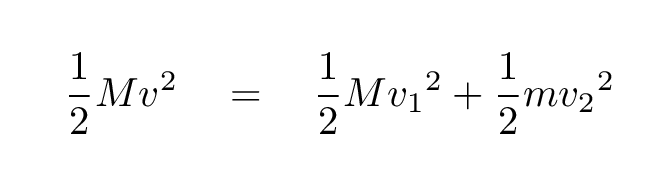
Q: Can you solve for the final velocities
v1 and v2?
Well done!
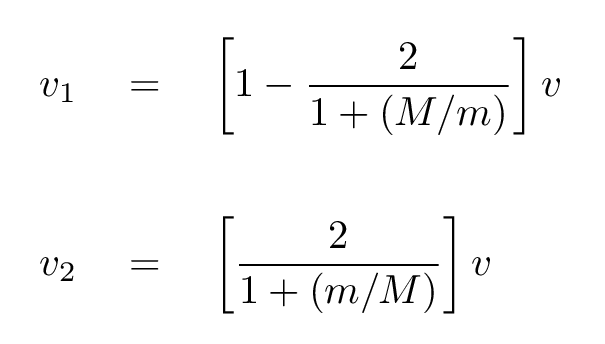
Now, suppose that, as in the real case, the big object (Jupiter) has a much, much, much larger mass than the small object (Voyager). The expressions for these final velocities can be simplified.
Q: Can you simplify these expressions if M >> m?
Right.
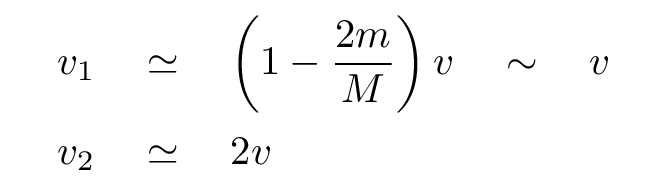
So, if a very massive object moving with initial speed V runs into a stationary, very-low-mass object, the low-mass object will shoot away from the collision with a speed of about 2*V.
Consider Voyager 2 as it approaches Jupiter. It's moving pretty slowly at this point, while Jupiter is speeding past in its orbit. (Click on image to watch movie)
Before the encounter, the speeds of the two bodies relative to the Sun are
Voyager: 10,500 m/s
Jupiter: 12,240 m/s
After the "collision", Voyager 2 is thrown outward and forward, roughly in the direction that Jupiter was heading. A few weeks later, it has
Voyager new speed: 19,820 m/s
Voyager dist from Sun: 5.53 AU = 8.27 x 1011 m
Hey, that new speed isn't twice the speed of Jupiter.
Q: Why is the new speed of Voyager 2 somewhat less
than double the orbital speed of Jupiter?
Well, let's use those numbers:
Voyager new speed: 19,820 m/s
Voyager dist from Sun: 5.53 AU = 8.27 x 1011 m
Q: What is Voyager's KE (relative the Sun) now?
Q: What is Voyager's GPE (relative the Sun) now?
Q: How far from the Sun can Voyager 2 go now?
Not only did Voyager 2 pick up kinetic energy from this "collision" with Jupiter, it also -- thanks to the careful action of the JPL scientists -- was pushed in EXACTLY the right direction to end up passing Saturn!
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.