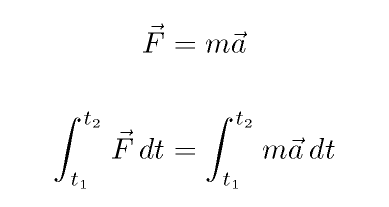
 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
So far, we've applied two sets of tools to understand what happens when objects interact:
But there are some very common, very important situations in which we need a new tool -- momentum.
Let's look at things in a bit of detail ..
You know some equations which connect changes in velocity to forces and accelerations .... but that isn't the complete story. Do your kinematic equations help you to answer this question:
I'm driving a car at 55 mph along the highway. How big a force will it take to stop me and my car?
The answer is -- it depends.
Your kinematic equations assume that the force is constant in size; what if it isn't? We can still use Newton's Second Law to say something about the behavior of the object under a time-variable force:
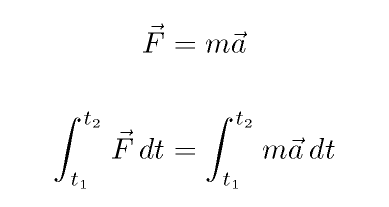
As long as the mass of the object(s) doesn't change, then we can take the m out of the integral:
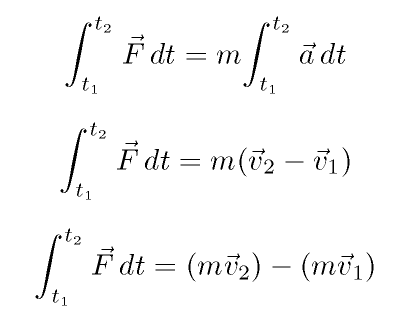
And now, if we define momentum p as the product of mass and velocity, we have
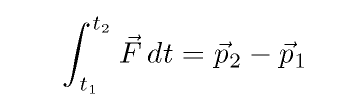
In words, we can say that
the change of a body's momentum is equal to the integral of the forces on it over time
Some guy named Newton wrote something along these lines:

Physicists have given the name impulse to the quantity "force integrated over time". Today you will use impulse to solve some problems.
Note one special case: if the magnitude of a force is constant, then its impulse is simply the force multiplied by the time it acts.
Momentum turns out to be enormously useful in solving problems which involve collisions, even when you don't know the details. Why? Because under very common circumstances, the total momentum of a set of colliding objects will be the same before and after they collide; in other words, momentum is conserved.
In a collision, as long as there are no net external forces, momentum will always be conserved. That makes momentum a very powerful tool for dealing with collisions. Kinetic energy, on the other hand, is not always conserved in collisions. Given the choice, then, it's usually better to try using momentum than kinetic energy if you face a complicated collision between several objects.
 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.