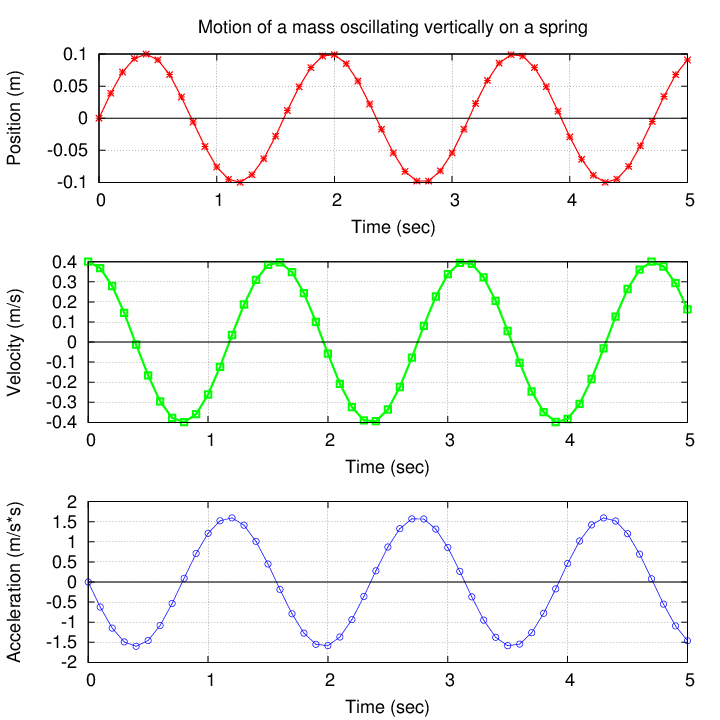
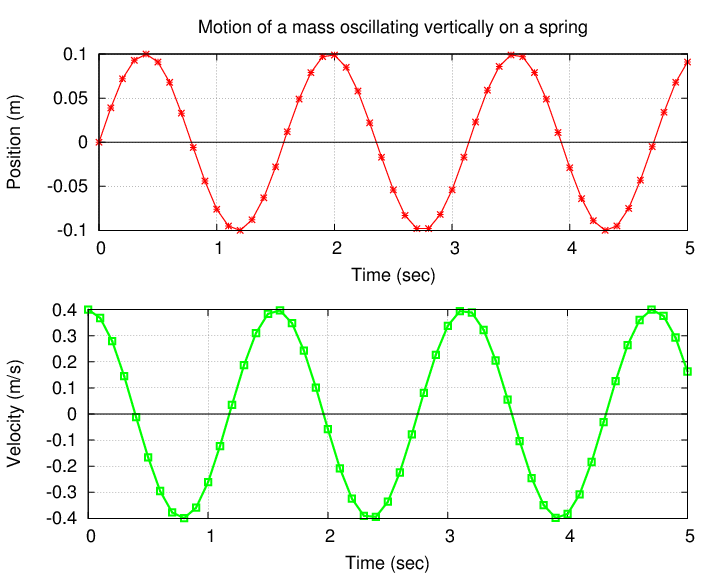
So, you've set up and measured the position of a mass bobbing up and down on a spring, as a function of time. Your measurements look like a sort of sinusoidal function. (I'm providing some sample data here, but you should look at YOUR measurements as you think about these questions).

We can describe this data mathematically as a sine function. For simplicity's sake, I've chosen data which just happens to start at x = 0 when t = 0, but we could still use a sine function even if it didn't; we'd just have to add a phase constant.
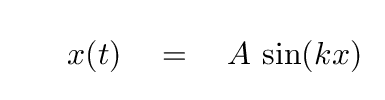
Now, there's a simple relationship between position and velocity, IN THEORY: the velocity is just the derivative of position as a function of time. Note that this would make the velocity no longer a sine function, but a cosine function. Hmmmmmm....
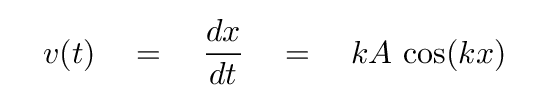
Look at your measurements. Do the velocity values "line up with" the position values, so that the peak of position occurs at the same time as the peak of velocity? Or is there some offset between them?
There is another simple relationship between velocity and accelerationu again, IN THEORY: the acceleration is the derivative of velocity as a function of time. Note that this would make the acceleration switch back to a sine function ... but with a negative sign out front. Hmmmmmm....
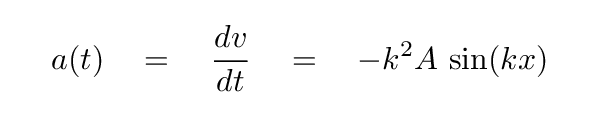
Look at your measurements. Do the acceleration values "line up with" the velocity values, so that the peak of acceleration occurs at the same time as the peak of velocity? Or is there some offset between them? And what about acceleration and position -- do THEY line up?