Preparing for the Conservation of Energy exercise

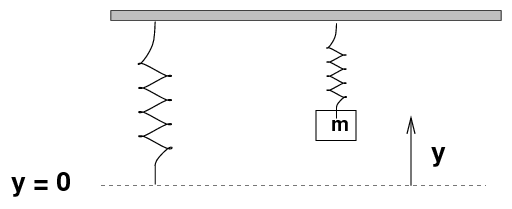
Consider a spring hanging at rest from a rod. If left to itself, it has some rest length. We could define a coordinate system based on vertical distance y above this rest length.

Suppose that we attach a block of mass m to the spring, and then we push this block up a distance y, compressing the spring.

What is the spring potential energy now?
What is the gravitational potential energy of the block now?
Write down the total potential energy of the system.

The total potential energy of the system is an expression with two terms --- right?

Now, let us allow the block of mass m to pull the spring down until it reaches an equilibrium point. At this point, the end of the spring is a distance L below the rest length.

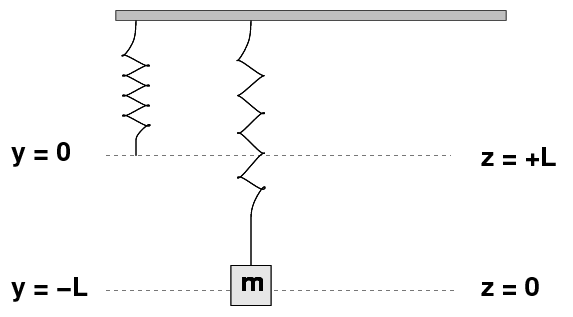
Solve for the magnitude of the equlibrium distance L in terms of m, g and the spring constant k.

Now, suppose that we instead decide to measure distances from this equilibrium position. (It will turn out to make our calculations simpler if we do this.) We'll use the coordinate z to denote "distance above the equilibrium position."

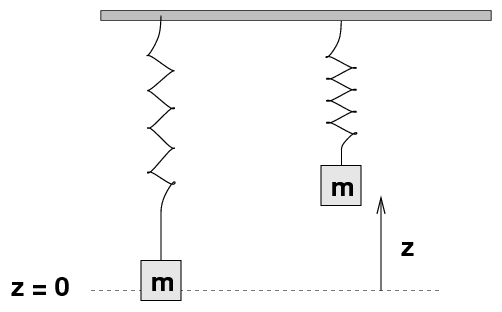
Write an expression for y in terms of z.

Now, we lift the block up from its equilibrium position by a distance z. What is its total potential energy now?

Use the expression for total potential energy you wrote in step 3, but convert from using the variable y to the variable z, using the expression you derived above.

This expression should have one term that changes with the position z, plus one term that is a constant.