 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Investigate the effect of elevation angle on projectile motion
Your job in this exercise is to watch very carefully as a
ball is shot out of a gun, flies through the air,
and lands on the floor.
After you have analyzed its motion, you must predict
where and when
the ball will land when shot at a different angle.
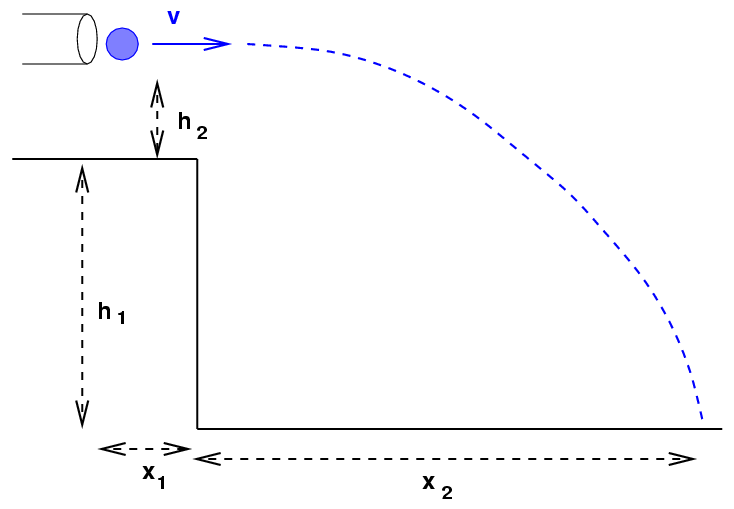
Here's the basic setup:
The two groups sitting at each table will share measurements
during today's exercise.
Each table will set up
a single cannon
on their table.
Remove the barrel of the gun from
the apparatus and re-set it onto the upper
portion so that it is horizontal.
Fire the cannon at its "medium range" setting.
Measure the time of flight in each case.
Make three trials and determine the average
distance the ball travels.
Each group independently must
- using the height H (= h1 + h2)
and total length L (= x1 + x2),
determine the speed v
at which the ball leaves the cannon.
- compute the uncertainty in the initial speed v.
- calculate the time of flight t of the ball.
Does it match your measurements?
Discuss.
- Now, suppose we change the angle of the barrel to
theta = 65 +/- 3 degrees.
Predict
At this point, call an instructor over. Show him your
work. When he verifies the information,
you may continue.
- Reset the cannon so that the angle
of the gun is
theta = 65 degrees.
You will need to remove the gun barrel from the
post and reverse it in order to tilt the barrel
and fire upwards at 65 degrees.
- Fire the gun three times;
each time, measure the horizontal
distance travelled and the time of flight.
- Does the actual horizontal range agree
with your predictions within the uncertainties?
If not, what do you think is the
single largest reason for the difference?
Be quantitative.
- Does the actual time of flight agree
with your predictions within the uncertainties?
If not, what do you think is the
single largest reason for the difference?
Be quantitative.
- Replace the gun barrel into its original, horizontal
position on the other side of the post.
 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.

 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.

 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.