 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Your job in this exercise is to watch very carefully as a ball is shot out of a gun, flies through the air, and lands on the floor. After you have analyzed its motion, you must predict where the ball will land when shot from a slightly different location.
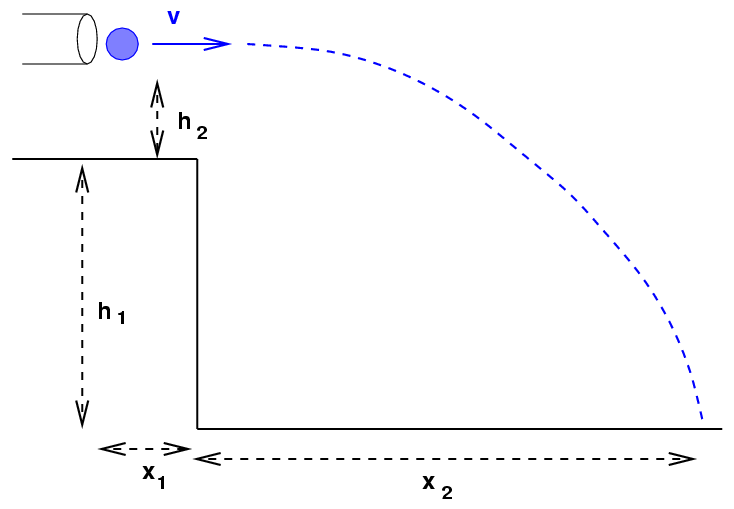
Here's the basic setup:

I'll place one of the ballistic pendulum devices on the table at the front of the room. We'll write the values of the heights h1, h2 on the board, then fire gun. I'll measure the distances x1, x2 and write those on the board, too.
Near the end of the class, I'll move the gun to one of the student tables and fire it. Your score will depend on how well your prediction and its uncertainty matches the actual distance.
How do you deal with combining two measurements, each of which has an associated uncertainty?
 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.