 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
You have a set of rings of different sizes:

You hang each ring from a pencil or pen and pull it gently to one side, then release it. The ring swings back and forth ...
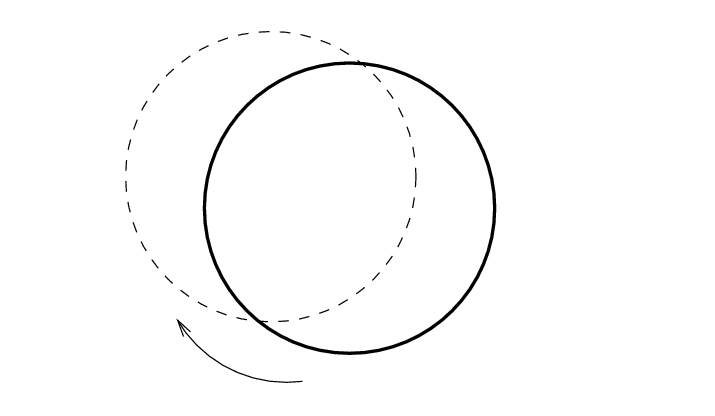
The goal is to figure out how long it would take a very large ring to complete one oscillation, based solely on the properties of the smaller rings.
Let's use this experiment to discuss some simple statistical notions, including the calculation of mean and standard deviation from the mean .
I did this experiment, too. For a ring of diameter d = 7.7 cm, I measured the following times for 10 complete oscillations (that is, 10 back-and-forth swings).
trial 1 5.46 sec trial 2 5.28 sec trial 3 5.29 sec
So, what can I conclude about the time it takes this ring to make 10 oscillations? If all the values were identical, I might say, "Aha, this ring takes exactly 5.46 seconds." But each trial was a little different.
In a case like this, when we have repeated measurements of what ought to be the same quantity, scientists often choose to describe the entire set of measurements with two numbers:
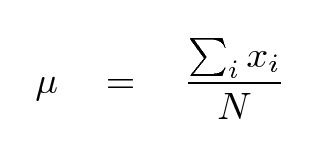
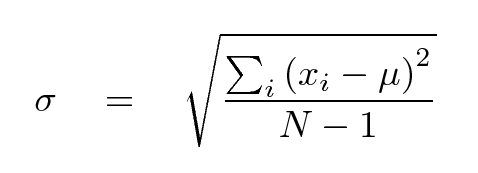
If you take a statistics class -- which would be a very good idea, at some point in your academic career -- you might learn about some of the delicate points that I've ignored in this brief introduction. For our purposes in this course, they aren't important.
Look again at my measurements. Can you compute the mean and standard deviation for the time it takes this ring to oscillate 10 times? Perhaps your calculator will do this for you ...
trial 1 5.46 sec trial 2 5.28 sec trial 3 5.29 sec
Here are the results from my calculations.
μ = 5.343 sec
σ = 0.101 sec
Does this mean that we should write the following?
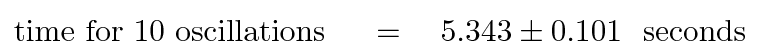
NO!
There are many possible values which lie within the stated uncertainty. Here are just a few:
5.356 5.287 5.371 5.402 3.328 5.396 5.276 5.415
What do these values have in common?
But the digit in the hundredth's place is pretty much random, as is the digit in the thousandth's place. It doesn't make sense to write a result which includes a digit in those places, because we really have no idea which digit it is.

So, let's get rid of all the "insignificant" digits -- the ones whose values we really don't know at all.

Oh, and if we remove those digits from the mean value, we should also remove the corresponding digits from the uncertainty.

So, the proper way to write the time it takes for the ring to make 10 oscillations is 5.3 +/- 0.1 seconds .
Your job: make a new table, in which you list the results of your own measurements. Compute the mean and standard deviation for each ring you measured, and write those values with the proper number of significant figures.
We want to find the period of oscillation of a really big ring, but all we know are the periods for a set of small rings. What can we do?
For example, suppose that our measurements looked like this:
diameter (cm) period (s)
-------------------------------
5 1.0
10 2.0
15 3.0
20 4.0
-------------------------------
Q: Can you predict the period of a ring of diameter 45 cm?
Well, sure. There's an obvious relationship, which we can express as an equation, like this:
1 s
Period (s) = Diameter (cm) * ---------
5 cm
or as a graph, like this:
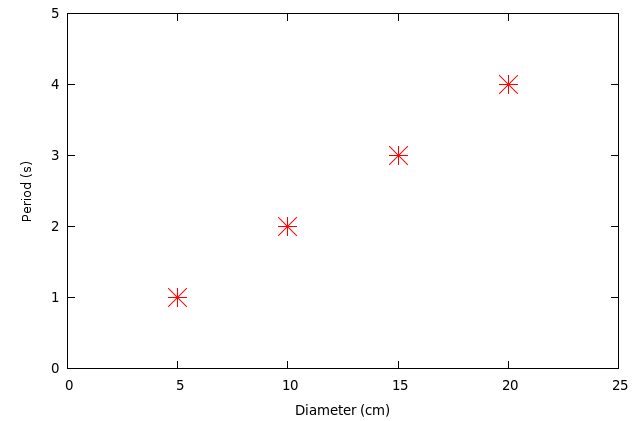
Q: What is the connection between the equation and the graph?
 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.