Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Standing waves on a string
Your job today is to predict the frequencies required to
set up standing waves on one (or two) strings, and compare
those predictions to reality in an experiment.
You must hand in a report which addresses all the items below,
with any graphs, pictures, and calculations required.
Staple your report pages together and place them in your folder
before you leave.
Neatness counts.
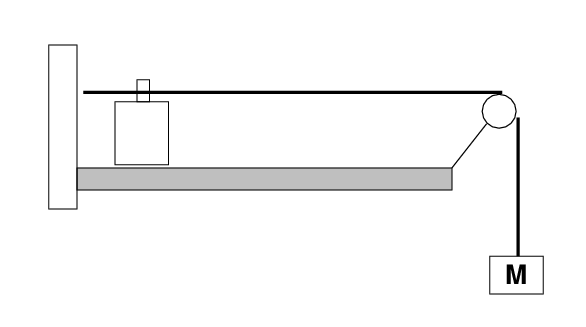
Using elastic cord ....
First, measure some properties of the elastic cord.
You'll need to include uncertainties in just about every quantity.
- Hang a mass of M = 750 g by the cord over the pulley.
Place tiny marks on your cord at the location of the vibrator
and the pulley.
- Measure the distance between the marks on your cord
when the cord is unstretched, and when
it is stretched between vibrator and pulley
with 750 g hanging from it.
- You can find several pieces of cord on the table at the middle of the
room. Determine the linear mass density of unstretched cord
using one or more of those pieces.
- Compute the linear mass density of your cord when it is
stretched and holding 750 g. Include an uncertainty.
- You should now be able to compute the speed
of waves travelling down the stretched cord,
and an uncertainty in that speed.
- Predict the four lowest frequencies (with uncertainties)
which should yield
standing waves on the stretched string.
Draw pictures of each wave.
Stop and show your work to an instructor. When he approves, continue.
- Using the function generator and amplifier, measure the
actual frequencies which yield the four waves you predicted above.
Include an uncertainty.
- Do your predictions agree with the actual frequencies,
within their mutual uncertainties?
If you find a systematic difference, call the instructor over
to discuss it. There may be an explanation ...
If you have time, do the next part ....
Using fishing line ....
Now, let's repeat the experiment with a very different type of
string. The fishing line is (for our purposes) a fixed length
under any tension.
But since the fishing line is much lighter than the cord,
we'll change the hanging weight so that its mass is m = 200 g.
- Cut a piece of fishing line long enough to replace the
elastic cord.
Measure its mass and unstretched length.
Compute its linear mass density, and the uncertainty therein.
- Assume that the stretched mass density of the line
is the same as its unstretched mass density.
- Compute the speed
of waves travelling down the fishing line
when it supports a 200 g weight,
and an uncertainty in that speed.
- Predict the four lowest frequencies (with uncertainties)
which should yield
standing waves on the fishing line.
Again, draw pictures of each wave.
Stop and show your work to an instructor. When he approves, continue.
- Leave the elastic cord attached to your aluminum rod!
Slide the other end of the cord off the hanging weights.
- Tie one end of the fishing line to the rod (above the cord),
and the other end to the weights.
- Using the function generator and amplifier, measure the
actual frequencies which yield the four waves you predicted above.
Include an uncertainty.
- Do your predictions agree with the actual frequencies,
within their mutual uncertainties?
If you find a systematic difference, call the instructor over
to discuss it. There may be an explanation ...
If you have more time ...
- Set up a standing wave with 10 nodes in the elastic cord.
How close is the actual frequency to the predicted frequency?
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.