Power transmitted by a wave

How much energy does a wave carry as it moves through some material? Or, to put it a slightly different way, how much POWER does a wave deliver to some material as the wave passes through it?

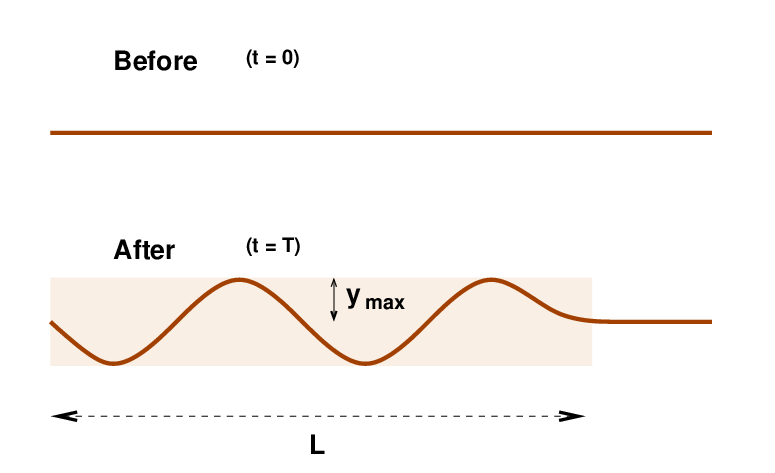
Imagine a piece of string, with linear mass density μ kilograms per meter of length, just sitting motionless. It has no energy. Boring.

Then, suddenly, a wave approaches from the left. It zips along the string, from left to right, at some speed v. After the wave reaches a bit of string, that bit starts to oscillate in the vertical direction with some amplitude y_max and angular frequency ω.

The pieces of string which have not YET been touched by the wave remain at rest.

The pieces which are oscillating vertically can be described like so:

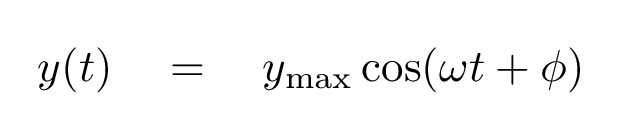
Can you figure out the SPEED of these pieces of oscillating string, as they move in the y-direction?

Right. It's just the derivative of the position in the y-direction with respect to time.

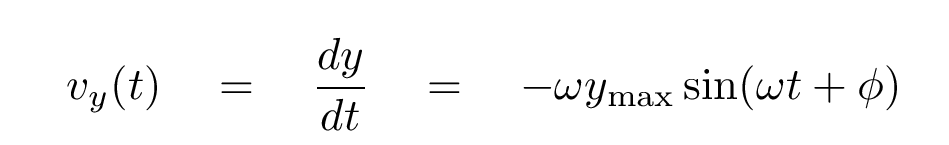
So, what's the maximum kinetic energy of one chunk of string as it oscillates?

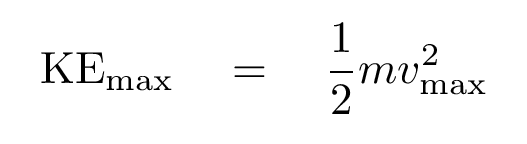
Not all of the string is moving at its maximum speed at any one time, of course; most of it is moving more slowly. But in addition to the kinetic energy, the wave imparts potential energy to the material. As time passes, the energy of any one little section switches between kinetic and potential, kinetic and potential, back and forth. If one looks over a long period of time, the total energy of any piece is equal to the maximum kinetic energy it ever reaches, which is the same as the maximum potential energy it ever reaches. So we can write

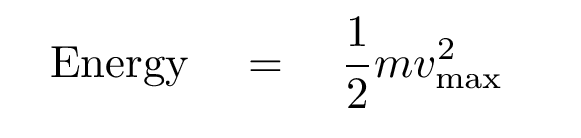
Okay, good. Can you figure out the maximum value of the string's speed in the y-direction, and then plug that into this equation for the energy of the string in the oscillating region?

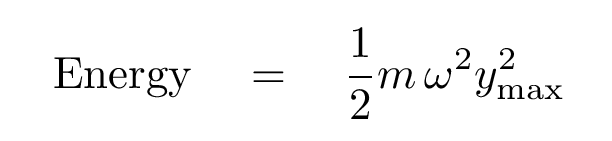
We are almost to the end of figuring out the power carried by the wave. One of the final steps is to figure out how much mass the wave has set into motion.

Look at the picture above. The linear mass density of the string is μ. What is the mass of the string which has been set into motion during the time interval from t = 0 to t = T?

Yes, of course. The length of the section touched by the wave is m = v T, where v is the velocity of the wave. That means that the energy given to this section of the string during the time interval must be

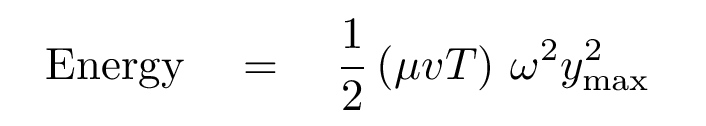
Right. One last step. We need to convert the ENERGY of this section of the string into the POWER which has transmitted by the wave. Hmmm, energy and power -- how are they related?

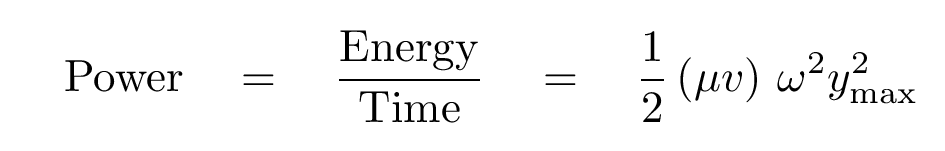
That's fine. It's correct. But it's not the only way to write the result.

You may recall that there is a relationship between the angular frequency ω of a wave and the speed of its pattern v in the direction of propagation.

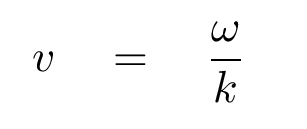
If we replace the v in our equation for power carried by a wave with this expression, then the power becomes

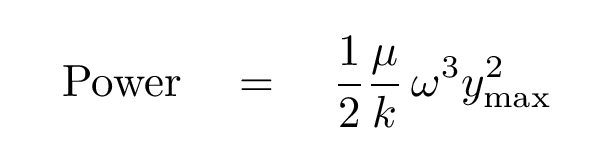
Let's do an example to see how all this works.



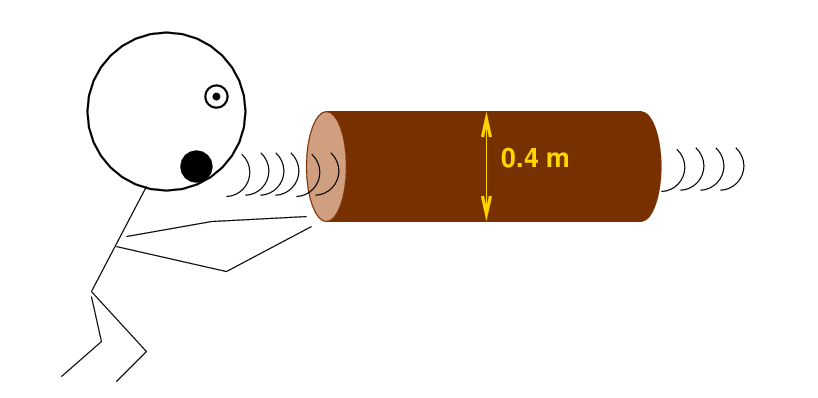
        Joe sings into a long cardboard tube of radius r = 0.2 m.
        He hits a perfect middle C (256 Hz), causing the air
        molecules to shake back-and-forth.  At the far end of the
        tube, the sound wave carries a power of 0.0001 Watt = 0.0001 Joule/sec .

        How large is the amplitude of motion of the air molecules
        in the tube?