 Viewgraph 1
Viewgraph 1
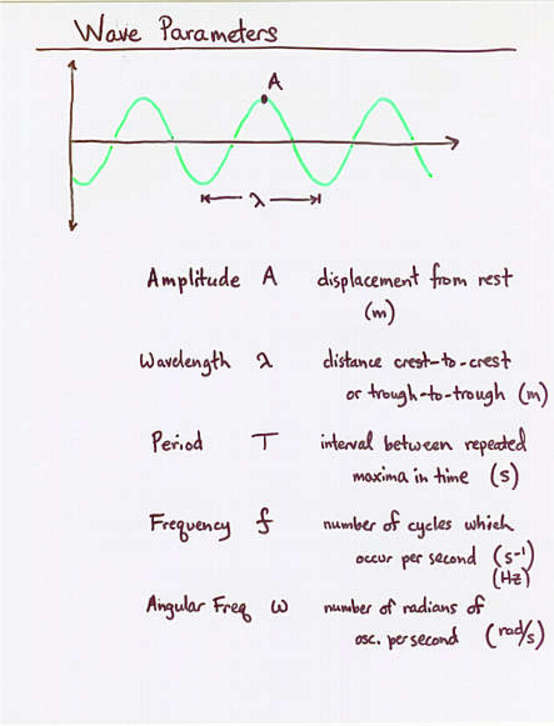 Viewgraph 2
Viewgraph 2
Don't forget k = wave number .
2 * pi
k = -----------
wavelength
 Viewgraph 3
Viewgraph 3
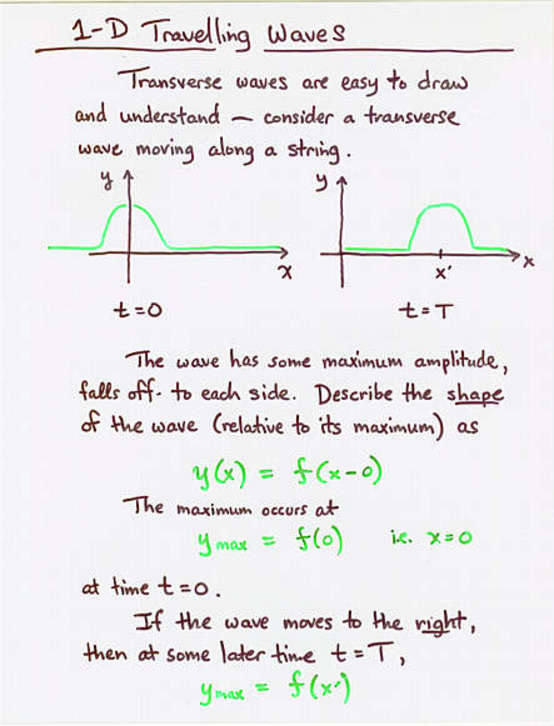 Viewgraph 4
Viewgraph 4
 Viewgraph 5
Viewgraph 5
 Viewgraph 6
Viewgraph 6
So, if we have a wave written in the standard form
sin (kx - ωt)
then the wave speed will be
ω
v = ---
k
 Viewgraph 7
Viewgraph 7
Challenge Problem: An earthquake hits Los Angeles! A wave ripples down the LA Freeway at a speed of 150 mph, with crests 60 m apart. Motorists caught by the quake are shaken up and down inside their cars violently. The road moves so quickly that, after pushing cars up to a peak height at a crest, the asphalt almost leaves the tires behind as they fall into a trough.
Write an equation for this wave of the form
y(x, t) = A * sin ( k*x - omega*t )
but provide the numerical values for all constants,
in standard SI units.
Now is a good time for physlets ....
 Viewgraph 8
Viewgraph 8
 Viewgraph 9
Viewgraph 9
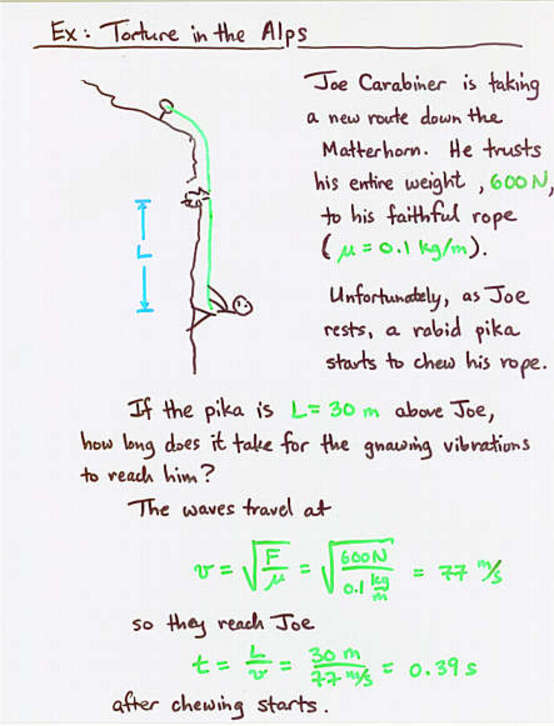 Viewgraph 11
Viewgraph 11
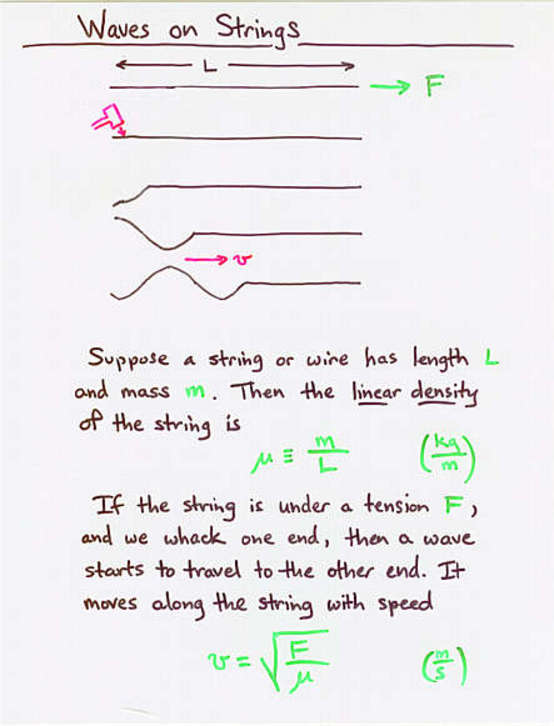 Viewgraph 10
Viewgraph 10