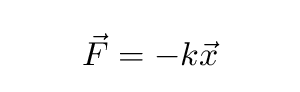
 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
The simplest case is a simple harmonic oscillator, which responds to a simple force:
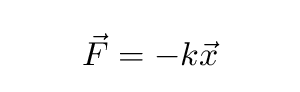
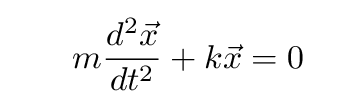
The solution to this differential equation is a sine or cosine function which oscillates with a natural frequency ω0
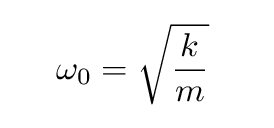
If we add a resistance which depends on velocity,
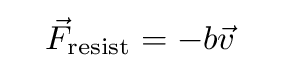
the equation of motion grows a bit:
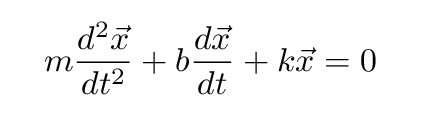
(I'm going to get rid of the vector signs at this point, for simplicity)
Now, let's add something new: a driving force with magnitude Fd (the subscribe d stands for "driving") which varies sinusoidally with angular frequency ωd. That means that Newton's Second Law for the object becomes
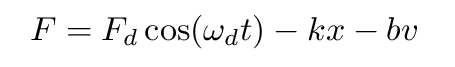
Or, if we write this as a differential equation for the position of the object as a function of time, x(t), we have
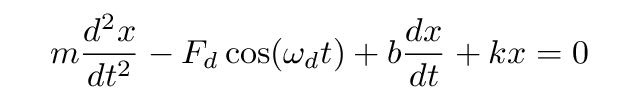
Now, we can guess a solution to this equation and work out the details, just as we did earlier.
Just kidding.
The general solution to this equation is .... messy. It consists of several terms. Some of those terms, however, include negative exponential factors of time, and so decay as time progresses. If we ask "what is happening after some long time passes?" we find that the steady state can be described by a simple formula:
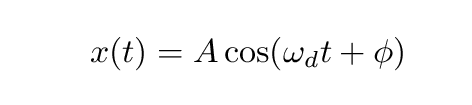
It should be no surprise that the object will oscillate with a frequency that matches the driving force; after all, the driving force is, well, DRIVING the object.
What is more interesting is the SIZE of the oscillations. Their amplitude, written above as simply A, actually depends on a combination of the driving frequency and the natural frequency ωo of the object itself.
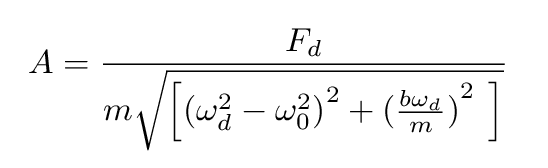
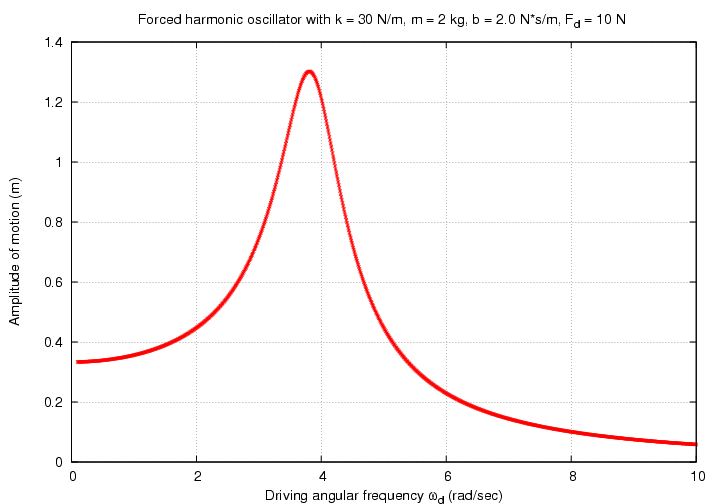
Note that the amplitude of motion depends crucially on how far the driving frequency is from the natural frequency.
Look at the equation for the amplitude again:
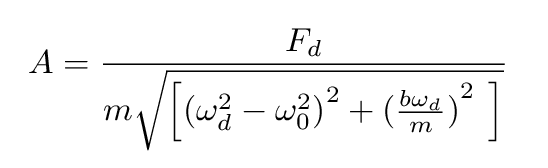
Suppose that the coefficient for "friction" or "resistive" velocity-dependent force, b, is ZERO -- in other words, that there is no dissipation.
Q: What happens to the amplitude if the driving frequency
is exactly equal to the natural frequency?
Resonance occurs when the driving frequency ωd is equal to the natural frequency ωo of a system. Every little forward push applied by the driving force happens as the object is moving forward, and every little backward pull applied by the driving force occurs as the object is moving backward. That means that the WORK done by the driving force on the object is always positive
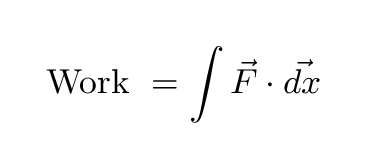
and so the driving force transfers energy to the object very efficiently.
You all have experience with driving forces and resonance, even if you don't realize it.

Engineers who design buildings and bridges must figure out AHEAD OF TIME the resonant frequencies of their structures, and make sure that these frequencies are far from any which might be excited naturally by earthquakes, traffic, wind, columns of marching soldiers, rock bands, and other primal forces.
 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.