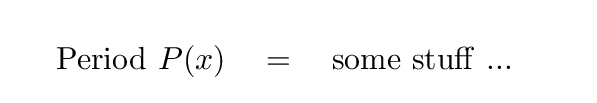Optimizing a Physical Pendulum
First, let's set up and measure the motion of a physical
pendulum. Set up at your table a device
which suspends a meterstick from a hole located
a distance x from its center.
The instructor will provide the values of x for each group
of students.
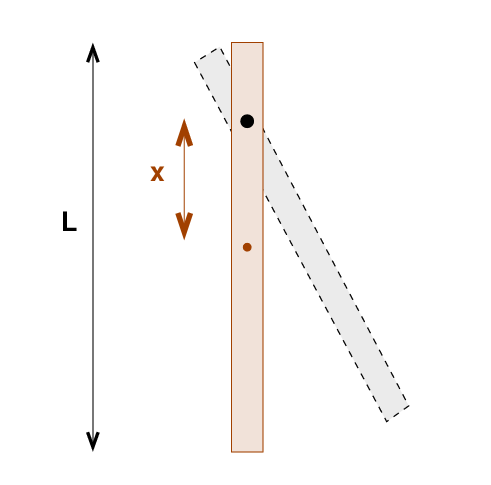
You must make sure that your meterstick is free to
rotate around the pivot point.
If there is too much friction,
let me know.
Experiment
- Measure the period of oscillation of the meterstick
for three values of x
(which your instructor will provide to each group).
Make three trials at each value
- Compute a mean period for each value of x.
- Compute the uncertainty in the mean period for each value of x.
- Make a neat table which shows the periods and uncertainties
which you measured.
- Write your values on the board at the front of the room
Theory
Your next job is to figure out what the period of oscillation
ought to be
for any given value of x.
- Compute the moment of inertia of the meterstick
around its pivot point for an arbitrary
offset distance x.
Leave your answer in symbols
such as M, L, and x.
- Compute the torque around the pivot point
for an offset distance x,
when it has swung an angle θ
away from the vertical. You will need
to include g, the acceleration due to gravity.
- Write an equation which gives the angular
acceleration of the meterstick
as a function of the angle θ.
- Assuming that the angle θ is small,
much less than 1 radian,
write a differential equation which
relates the angular acceleration
to the angular displacement.
- Write an equation which gives the period
of oscillation for this offset x.
Experiment vs. Theory -- easy
- Compare your measured periods to the periods predicted
by theory.
Do they agree within the uncertainty in the measurements?
If not, explain why not.
Experiment vs. Theory -- hard
Look at the values of periods written on the board,
based on measurements by all the groups.
- Which offset distance x
(if any) yields the SHORTEST period?
Look at the equation you wrote
in response to question 10, above.
Make a graph which shows
period on the y-axis,
as a function of offset distance x
on the x-axis.
Use a range of
10 cm < x < 45 cm .
- Based on your graph, which offset should yield the SHORTEST period?
Now, look at the equation you wrote in
response to question 10, above.
It should have the form
"Period as a function of offset distance x equals .... ",
like this:
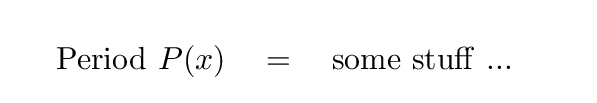
You may recall from a calculus class that you can find
the minimum value of a function by taking the derivative
and setting it equal to zero.
Let's try that:
- Write an expression for the derivative of P(x).
(This can get messy if you take the long route; ask for a hint)
- Find the value of x which makes this expression equal to zero
- How does this value compare to your EXPERIMENTALLY
determined best value of x?
- How does this value compare to your GRAPHICALY
determined best value of x?