 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Damped Harmonic Motion in action
I will set up a meterstick attached to a rotary-motion sensor
at the front of the room. The meterstick has a mass of
m = 0.137 kg
and is suspended by a hole which is
h = 0.30 m from its center.
I'll use the computer to record
the motion of this meterstick as it oscillates.
You will have to use measurements of
angular position as a function of time
to compare the theoretical behavior of this
meterstick to its real behavior.
Theory
- Compute the moment of inertia I of the
meterstick in units of (kg*m^2).
- What is the theoretical
angular frequency ω
of the meterstick if you
assume that there is no air resistance?
(Hint: write a formula relating angular acceleration
to angular displacement, then express the
angular acceleration in terms of torque and moment
of inertia; or see your textbook).
Real Life
- Download this file to your desktop
- Double-click on the file you have just downloaded ...
you should see LabPro start and show you
a screen with several panels.
- What is the MEASURED angular frequency
ω
of the
meterstick?
(Hint: count the number of oscillations it makes
over 20 or 30 seconds, and use the period to compute
ω
)
- How does the measured angular frequency compare to the theoretical value?
- Use the "Analyze -> Curve Fit"
command to fit a negative exponential function
to THE UPPER ENVELOPE of your measurements as a function of time.
-
Write down an equation of the form
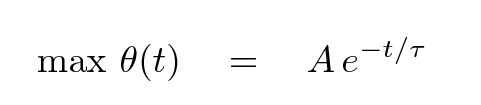
- What is the value of A? What are its units?
What does it represent?
- What is the value of
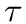 ?
What are its units? What does it represent?
?
What are its units? What does it represent?
Now, I attached a single paper "sail" to the meterstick,
to increase its area as it swings back and forth,
back and forth.
That means that with the sail, the
force of air resistance should be larger.
The mass of the paper in the sail is so small
compared to the mass of the stick that it can be neglected.
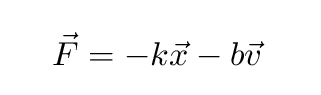
- Which term in the equation above should change due to the sail?
- What should happen to the angular frequency
ω
of the oscillations as a result?
- What should happen to the time constant
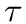 of the oscillations as a result?
of the oscillations as a result?
- Download these files to your desktop; it contains
measurements of the oscillation of the meterstick
when "sails" are attached.
- Analyze the motion of the meterstick with one sail attached.
- What is the angular frequency
ω
of the oscillations now?
Does this agree with your prediction in question 9?
- What is the time constant
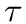 of the oscillations now?
Does this agree with your prediction in question 10?
of the oscillations now?
Does this agree with your prediction in question 10?
- Analyze the motion of the meterstick with TWO sails attached.
- What is the angular frequency
ω
of the oscillations now?
Does this agree with your prediction in question 9?
- What is the time constant
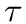 of the oscillations now?
Does this agree with your prediction in question 10?
of the oscillations now?
Does this agree with your prediction in question 10?
 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
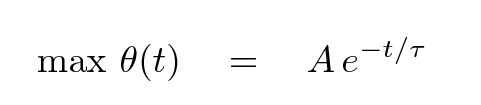
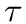 ?
What are its units? What does it represent?
?
What are its units? What does it represent? 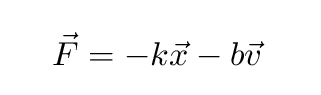
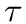 of the oscillations now?
Does this agree with your prediction in question 10?
of the oscillations now?
Does this agree with your prediction in question 10?
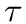 of the oscillations now?
Does this agree with your prediction in question 10?
of the oscillations now?
Does this agree with your prediction in question 10?
 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.