 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Rotation of a meterstick
We start with a meterstick -- one of the metersticks in
the classroom.
It has length L = 1.00 m and mass M = 0.150 kg;
we will assume that the density is uniform.
The stick has a number of holes drilled in it,
so that the stick can be suspended and rotated around
some point a distance x from the center
of the stick.
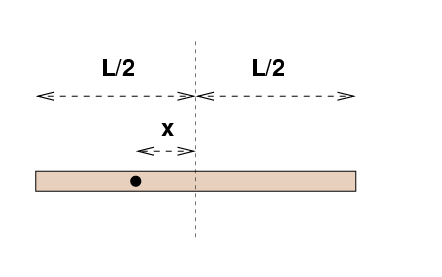
- What is the moment of inertia of the meterstick
for x = 0.20 m?
I will set up the meterstick so that it is originally
horizontal, then release it.
It will swing down, up on the other side, then
back down, etc.
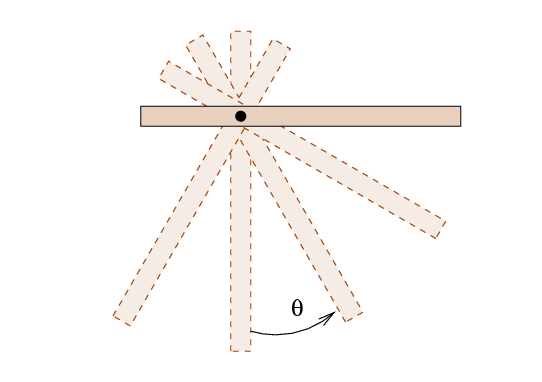
Let us begin in a generic sense ...
- Write a formula which shows the torque on the meterstick
when it is an angle theta from the bottom of its swing.
- Write a formula which shows the angular acceleration of the meterstick
when it is an angle theta from the bottom of its swing.
If you have time ...
- Suppose that the meterstick is moved to initial angle
thetamax and then released from rest.
Write a formula which shows the angular velocity of the meterstick
when it is at the bottom of its swing.
(Hint: it's easier to use energy than torque in this case...)
Now, let's get specific. For this particular meterstick,
make a table and a graph.
- make a table showing the angular
acceleration (in radians/sec) of the meterstick at angles
theta = 0, 0.10, 0.20, 0.30, 0.60, 0.9, 1.2, 1.5 radians.
- make a graph which shows angular acceleration (in rad/sec^2)
versus angular displacement (in rad),
over the range theta = -1.5 to +1.5 radians.
Plot the points from your table.
If you have time ...
- compute the maximum angular velocity of the stick
if it is released from
initial position thetamax = 0.20 radians
Look at your graph to answer these two questions.
- Is the angular acceleration always linearly related to the
angular displacement, or only over a limited range?
- Write an equation of the form
ang accel = (const) * (ang displacement)
Use your graph to find the value of the constant. What are its units?
 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.

 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.


 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.