 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.

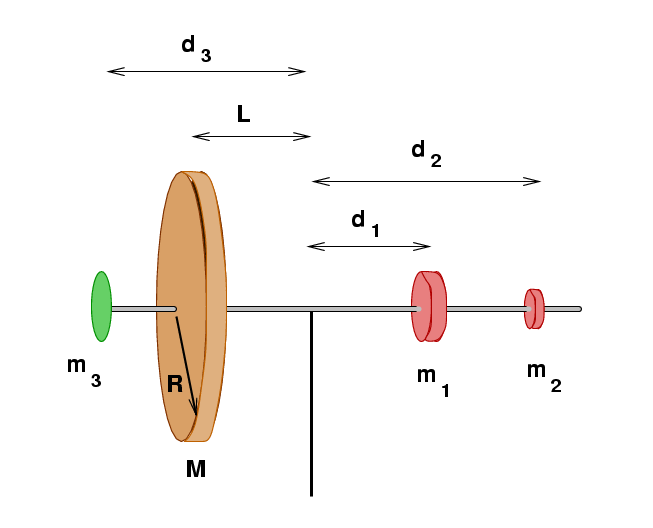
I have arranged a gyroscope at the front of the room in the manner shown above. We'll pretend that the rod connecting all the pieces is massless, and make a few other approximations along the way. We will use units of grams and centimeters for this exercise, so be sure to use g = 980 cm/s^2.
For our purposes,
component mass dist from axis
---------------------------------------------------------------------
disk M = 1700 g L = 14.1 cm R = 12.6 cm
weight 1 m1 = 900 g d1 = 25.3 cm
weight 2 m2 = 40 g d2 = 30.4 cm
weight 3 m3 = 50 g d3 = 19.5 cm
---------------------------------------------------------------------
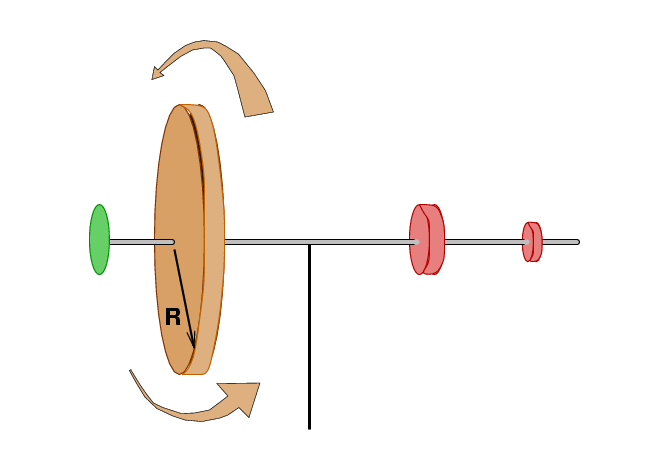
Now, consider the force of gravity. It pulls all four objects straight down: the three weights and the disk.
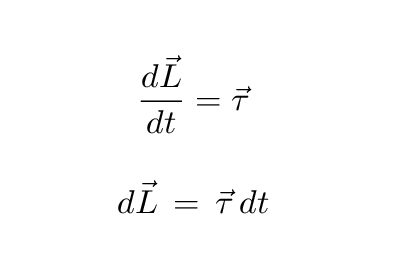
After just a very short time, the angular momentum will point in a slightly different direction.
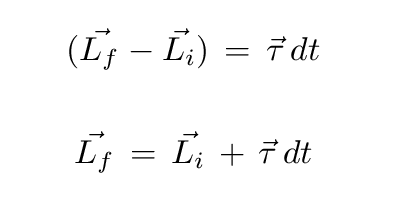
However, the magnitude of the angular momentum of the disk will not change (if we ignore the gradual slowing of the rotation due to friction and small effects).
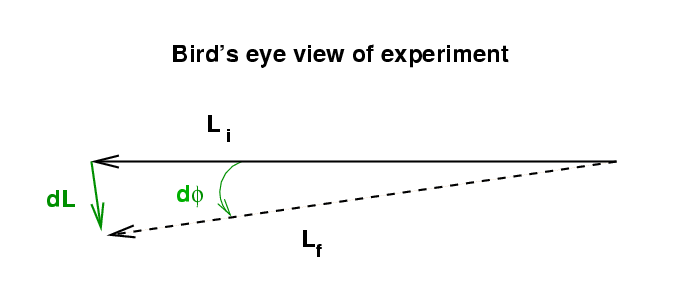
If we measure the little angle d phi by which the angular momentum vector has changed in radians, then the size of the change dL can be expressed as
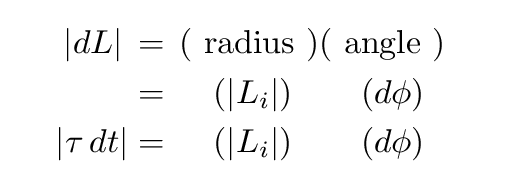
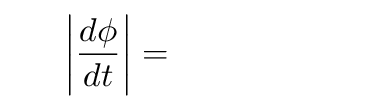
 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.