 Viewgraph 1
Viewgraph 1
 Viewgraph 2
Viewgraph 2
 Viewgraph 3
Viewgraph 3
 Viewgraph 4
Viewgraph 4
 Viewgraph 5
Viewgraph 5
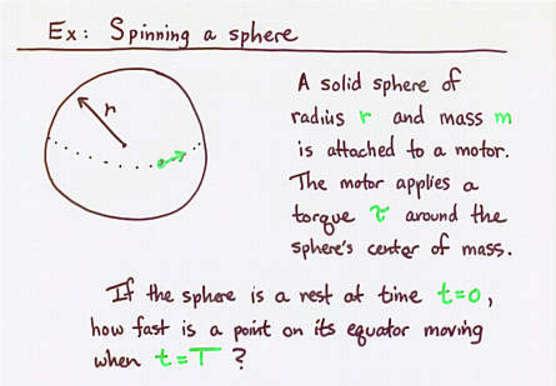 Viewgraph 6a
Viewgraph 6a
Given m = 500 kg, r = 10 m, torque = 600 N-m ccw,
can you figure out at time T = 10 seconds
a) the linear speed of a point on the equator?
b) the rotational kinetic energy of the sphere?
c) the angular momentum of the sphere around its center?
 Viewgraph 6b
Viewgraph 6b
 Viewgraph 7
Viewgraph 7
 Viewgraph 8
Viewgraph 8
 Viewgraph 9
Viewgraph 9
In this performance by Yu-na Kim at the 2013 Worlds (or you can see a local copy ),
- watch her spin at about 2:50 into the video
- watch her prepare for a triple jump, and then jump and spin, at about 0:50 into the video
Dorothy Hamill spins in the 1985 World Pros artistic program. (or look at local version ).
Stars form as large clouds of gas and dust collapse.

Image courtesy of
NASA/ESA/STScI/J. Hester and P. Scowen

Images courtesy of
NASA/JPL-CalTech/N. Evans and Spitzer Space Telescope
 Viewgraph 10
Viewgraph 10
 Viewgraph 11
Viewgraph 11
 Viewgraph 12
Viewgraph 12