Creative Commons License Copyright © Michael Richmond. This work is licensed under a Creative Commons License.

Problems involving conservation of angular momentum

  1. A solid disk is mounted on a frictionless bearing, so that it can rotate freely around its center. It is initially rotating with angular speed w. Alice takes a second circular object -- with the same mass and radius as the disk -- and holds it motionless. She then drops it onto the disk, so that it lands perfectly centered. After a bit of rubbing, the two objects end up rotating with a common speed of 1/3 w.

    What type of object did Alice drop onto the disk?

  2. Jogger Joe (of mass 60 kg) stands on his new Circular Treadmill (TM). It is simply a disk of aluminum, 5 meters in diameter and 10 cm thick, mounted on a frictionless bearing. Joe steps onto the disk carefully, so that he and the disk are at rest. Joe then begins to jog at the outer edge of the disk. After a while, he reaches a steady pace, so that the disk rotates once every 136 seconds.

    1. What is the angular velocity of the disk?
    2. What is the angular momentum of the disk?
    3. What is Joe's angular momentum around the center of the disk?
    4. What is Joe's angular velocity?
    5. How fast is Joe jogging? Compute the linear speed of his feet, relative to the disk.

    Answer to the treadmill problem

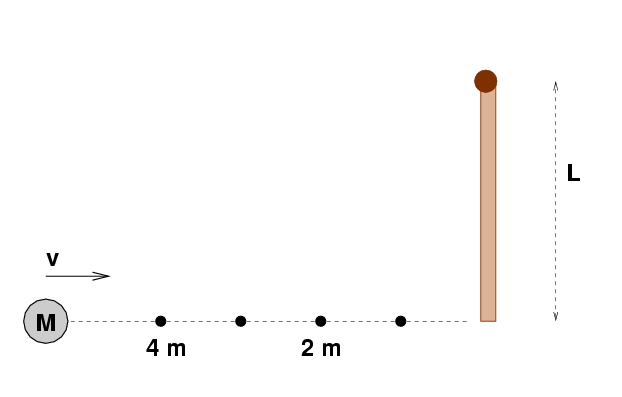
  3. The handle of a broken hockey stick, of length L = 1.3 m and mass M = 320 grams lies motionless on the ice. One end is pegged to the ice, but the stick is free to pivot around that point. A hockey puck of mass m = 160 grams slides across the ice towards the end of the rod with a speed v = 10 m/s.
    1. What is the total kinetic energy of the system as the puck approaches the stick?
    2. What is the angular momentum of the puck around the pivot point when it is 4 m from the stick?
    3. What is the angular momentum of the puck around the pivot point when it is 3 m from the stick?
    4. What is the angular momentum of the puck around the pivot point when it is 2 m from the stick?
    5. What is the angular momentum of the puck around the pivot point when it is 1 m from the stick?
    6. What is the angular momentum of the puck around the pivot point when it reaches the stick?

      7. The puck hits the end of the rod and sticks to it. The rod and puck start to rotate around the pivot.

    7. What is the angular velocity of the stick-plus-puck as they pivot?
    8. What is the rotational kinetic energy of the stick-plus-puck?
    9. Was kinetic energy conserved in this collision?

Creative Commons License Copyright © Michael Richmond. This work is licensed under a Creative Commons License.