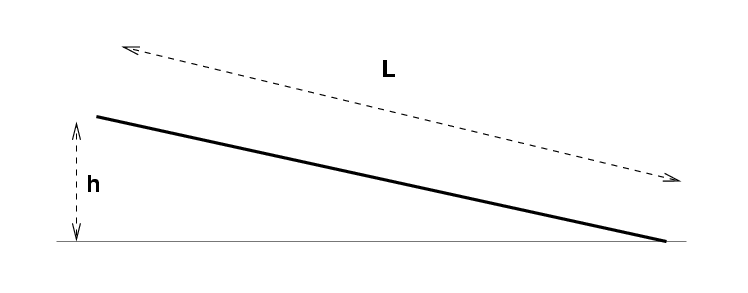
The table in the center of the room has a marked section which is L in length and rises h from end to end. We'll measure these values in class and write them on the board.

What is the acceleration of an object which slides down the table without friction? Express this acceleration in two ways:
- in terms of g, h, L
- in cm per second squared, plugging in the actual measurements
How long should it take for an object to slide without friction down the table? Again, express this
- in terms of g, h, L
- in seconds, plugging in the actual measurements

There are seven objects we will actually send down this table. They are:

lacrosse ball (solid)
can of Chunky Noodle Soup (full)
racquet ball (hollow)
soda can (full)
wooden disk
hoop
Hot Wheels Aston Martin V8 Vantage

For each type of object,
- write down the moment of inertia, in terms of M and R
- write the total kinetic energy (translational plus rotational) at the bottom of the table, in terms of M and the final translational velocity v
- solve for the final velocity v in terms of g, h
- solve for the time t it should take to reach the bottom, in terms of g, h, L
- write down an expression for the linear acceleration of the object, in terms of g, h, L
- plug in values to find time t in seconds
rank the objects based on the time they should take to reach the bottom of the table: fastest at the top, slowest at the bottom of the list

Near the end of the class period, we will actually send each object down the table and measure the time it takes to reach the bottom. You can then compare your predictions with the actual measurements.