Practice Problems for Test 3

  1. Joe has a barrel full of sand. The barrel is a cylinder L = 2 m long, with radius R = 0.5 m. The sand has density rho = 2000 kg/m^3. Joe suspends the barrel horizontally high above the ground so it is free to spin around its central horizontal axis.

    Joe wraps a rope several time around the barrel, and attaches the end of the rope to a bucket of mass m = 5 kg. The bucket hangs motionless H = 2.5 m above the ground because Joe is holding onto the barrel.

    At time t = 0, Joe releases the barrel. The bucket starts to fall downwards, pulling on the rope and causing the barrel to spin. As the bucket falls, the barrel spins faster and faster.

    How long does it take the bucket to reach the ground?

  2. A fancy flagpole consists of a uniform thin rod of length L = 5 m and mass m = 7 kg, and a compact gold ball of mass M = 2 kg. It is connected to the wall by a hinge at point P. A wire of length d = 4 m runs from the wall at an angle alpha = 70 degrees to support the pole.

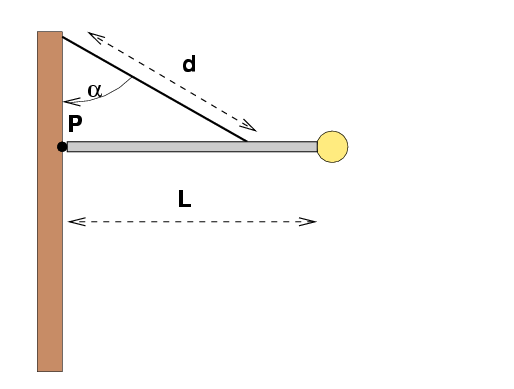
    1. When the flagpole is in equilibrium, what is the tension in the wire?

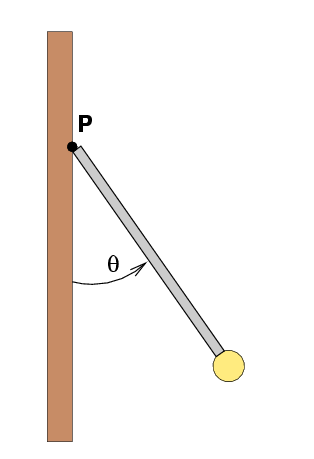
      2. The wire breaks! The pole starts to swing downwards around the hinge without friction of any kind.

    2. When the pole has swung so that there is an angle theta = 20 degrees remaining between it and the wall, what is the pole's angular acceleration around the hinge?

    3. Is the motion of the pole an example of simple harmonic motion?

    4. Just before the pole slams into the wall, what is the linear speed of the golden ball?

  3. Figure skaters Fred (mass mF = 60 kg) and Jane (mJ = 45 kg) prepare to spin together. They skate towards each other so that their outstretched arms (lengths AJ = 0.8 m, AF = 0.6 m) will just meet at the point marked "X". Their plan is to join hands so that they revolve around the point "X" without any translation.

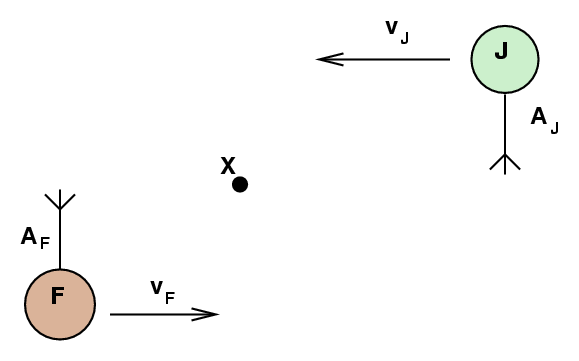
    1. Jane has initial speed 4 m/s. What speed should Fred have?
    2. What is their initial angular momentum around point "X"?

      3. It works! They are now holding hands and spinning around point "X", Jane AJ from the center and Fred AF from the center.

    3. What is their moment of inertia around point "X"?
    4. What is their angular speed?
    5. What are their linear speeds?
    6. What is their rotational KE?

      7. To end their program, they pull each other close, until their centers of mass are only bJ = 0.28 meters and bF = 0.21 meters from point "X".

    7. What is their angular speed now?
    8. What is their rotational KE now?

  4. Polly the Potter's wheel is made of solid steel (density ρ = 7780 kg/m^3 ), of radius R = 0.4 m and thickness h = 0.05 m. It is initially at rest.

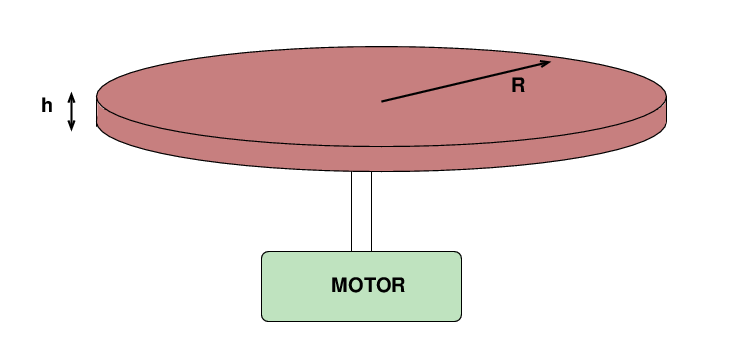
    Polly turns on the electric motor which is attached to her wheel. It applies a torque which increases gradually with time, according to the equation

    where time t is measured in seconds.

    1. What is the moment of inertia of the wheel?
    2. What is the torque at the time t = 2 s?
    3. What is the angular acceleration of the wheel at time t = 2 s ?
    4. What is the angular velocity of the wheel at time t = 2 s ?
    5. What is the instantaneous power delivered by the motor to the wheel at time t = 2 s ?

  5. A hungry pterodactyl of mass M = 3 kg soars with initial speed v = 10 m/s toward a giant swarm of locusts. The locusts float motionless in space, packed so tightly that their mass density is ρ = 0.08 kg/m^3.

    The pterodactyl opens its mouth wide, creating a circular maw of diameter D = 0.18 m. As it coasts into the swarm, it gulps down huge numbers of the insects. After a short time, its speed has been reduced to v' = 0.8*v = 8 m/s.

    (Assume that the pterodactyl is not flapping its wings this entire time, and ignore air resistance)

    1. What mass of locusts has the pterodactyl engulfed at this point?
    2. How far into the swarm has it flown?

  6. COBRA agent 59 throws a durian fruit at GI Joe from a distance d = 40 m. The M = 0.5 kg fruit heads straight toward Joe with a horizontal velocity of v = 25 m/s.

    Joe fires his trusty M16 at the incoming object. A bullet from his 5.56x45mm NATO cartridge (m = 4 grams) flies at w = 940 m/s toward its target, passes through it, and exits the fruit with a speed of w' = 600 m/s, still going in the same direction.

    1. What is the fruit's velocity now?
    2. How many bullets must Joe fire to stop the durian?

    (For fun)

    1. Does Joe have time to fire that many shots?
    2. What extra danger does Joe face due to his blowing holes through the durian?

  7. Fred makes a big flat disk of radius R = 0.9 m and mass M = 12 kg. He pins it to the wall with a pin in its very center, so that the disk is free to spin around the pin. Fred then glues to the outer edge of the disk a tiny blob of lead, with mass m = 0.5 kg. The lead hangs straight down below the pin.

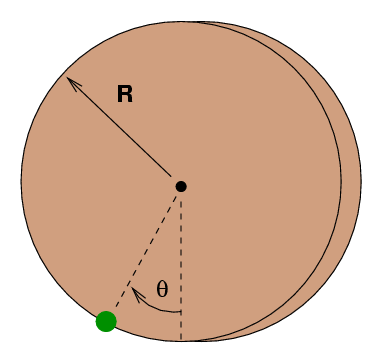
    Fred now turns the disk a small distance theta from its resting position and releases it. The disk starts to oscillate back and forth.

    1. Show that the motion of the disk is SHM.
    2. What is the period of the motion?