
 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Is it possible to measure the earth's radius -- armed only with a stopwatch? Yes! The answer will be only approximate, but that's a lot better than nothing.
The basic idea is to look at a sunrise or sunset (or moonrise or moonset) in a very particular manner:
The time it takes for the Sun (or Moon) to re-appear (or re-disappear) is related to the angle through which the Earth has rotated between (dis)appearances. If you can measure the time accurately, you can calculate the angle accurately. Use the following proportion:
time between disappearances angle through which Earth rotates
--------------------------- = ---------------------------------
one entire day 360 degrees
Okay, now what -- how can knowing the angle by which the Earth rotates help you to calculate the Earth's radius? Consider the following. Big Sam and Little Sam stand side-by-side to watch a sunrise. Big Sam is six feet tall, Little Sam is only three feet tall. Which one sees the sun first? Click on the figure below to find out...
Big Sam will see the Sun rise first, because his head will peek above the Earth's shadow first. Little Sam will have to wait for the Earth to rotate a bit farther in order for his head to rise above the shadow.
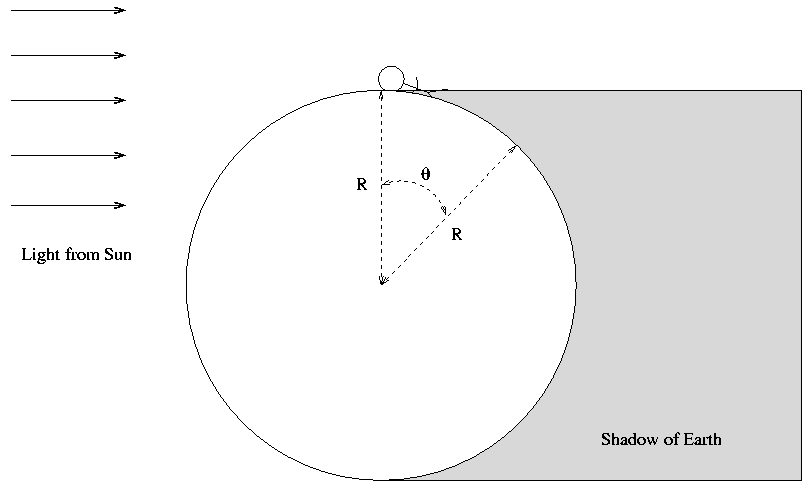
Exactly the same effect occurs when you watch a sunrise: there will be one particular moment when you are standing and just able to see light from the Sun.
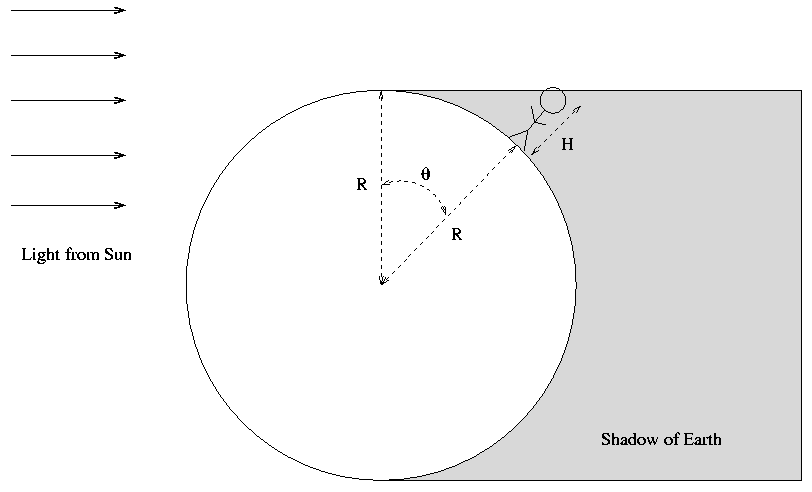
If you quickly lie down, so that your head is effectively at ground level, then the Earth will have to rotate an extra amount to bring you into the light:
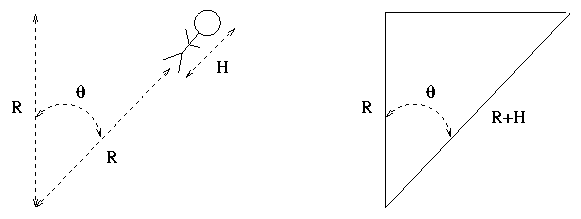
If you know that angle theta, and you know your height H, you can use a little trigonometry to calculate the radius of the Earth R.
Try it! If you have the opportunity, do this experiment several times on different occasions. How well do the results agree?
Will the answer you get depend on your latitude? All the diagrams I've drawn show the observers on the equator. Does it matter?
I welcome reports from anyone who has carried out this experiment. Please send your results to mwrsps@rit.edu and I'll include them in a later version of this page.
| Name | Angle (degrees) | Height (meters) |
| Marta R. | 0.04625 | 1.7 |
Last modified by Michael Richmond on Sep 9, 2009.
 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.