Magnetic Forces on Current-carrying wires

The magnetic force on a charged particle depends on the relative orientation of the particle's velocity and the magnetic field.
A magnetic force cannot change the speed of a charged particle, only its direction.
When a charged particle enters a uniform magnetic field in a direction perpendicular to that field, its motion is continuously changed by the magnetic force; it ends up moving in a circle, with radius
```
           radius = (mass * velocity) / (charge * magnetic field)
```
A current consists of many small charged particles running through a wire. If immersed in a magnetic field, the particles will be experience a force; they can transmit this force to the wire through which they travel.
The force on a section of wire of length L carrying a current I through a magnetic field B is
```
              F   =  I ( L x B )               vector version

                  =  I L B sin(theta)          strength only
```
where theta is the angle between the wire and the magnetic field. The direction of the vector L is the same as the direction of the current through the wire.
Because forces are easy to measure, it is the force exerted on a current-carrying wire which is used to define the SI unit of current, the ampere.

Viewgraph 1

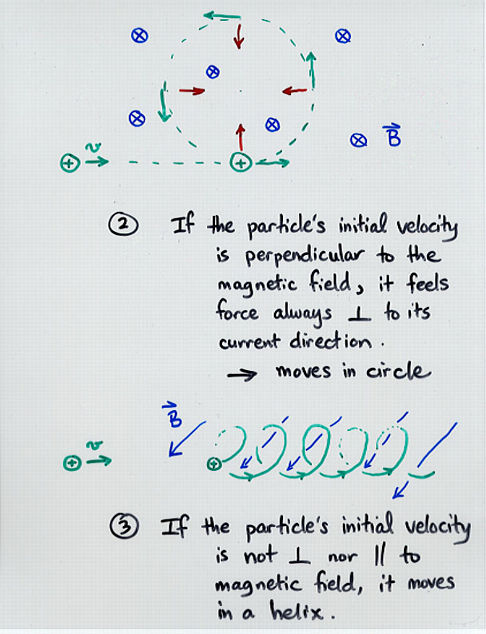Viewgraph 2

Viewgraph 3

Viewgraph 4

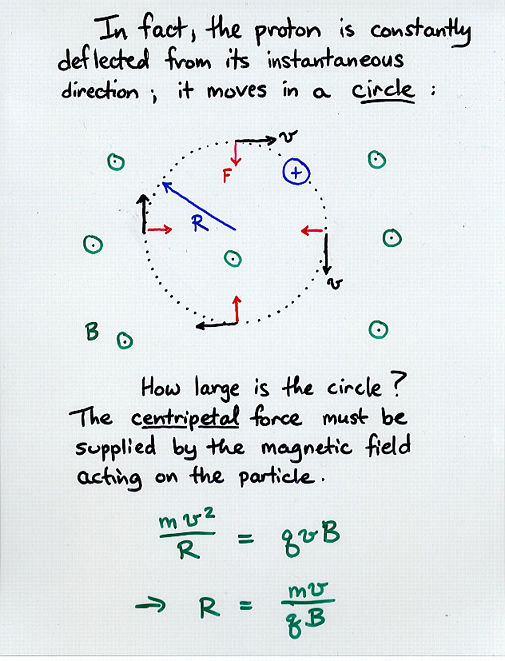Viewgraph 5

Viewgraph 6

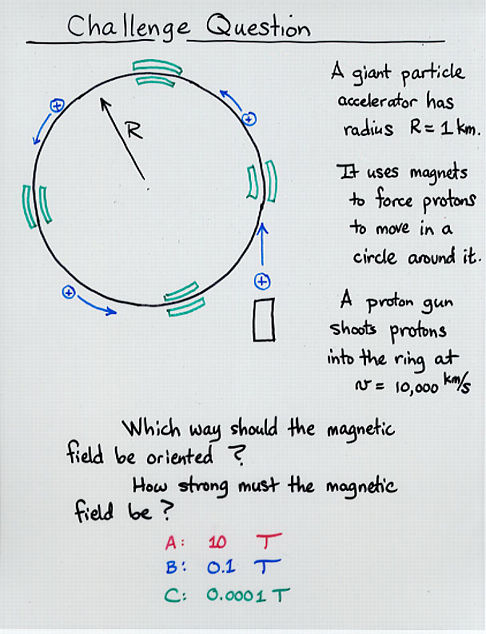Viewgraph 7

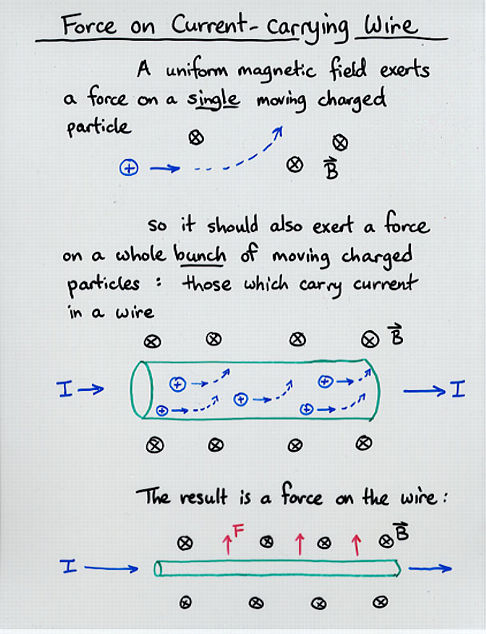Viewgraph 8

Viewgraph 9

Viewgraph 10

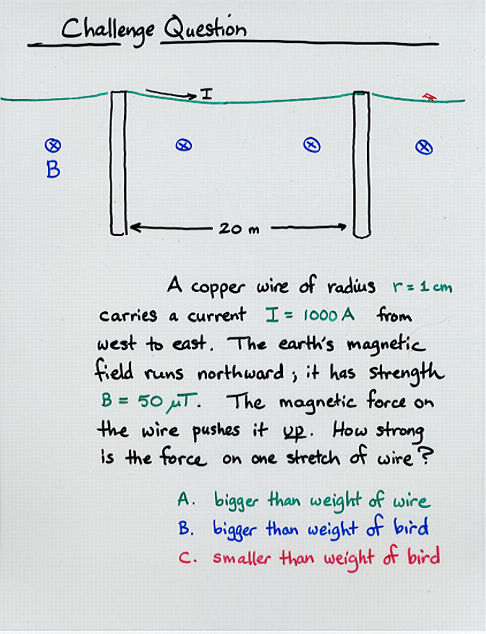Viewgraph 11

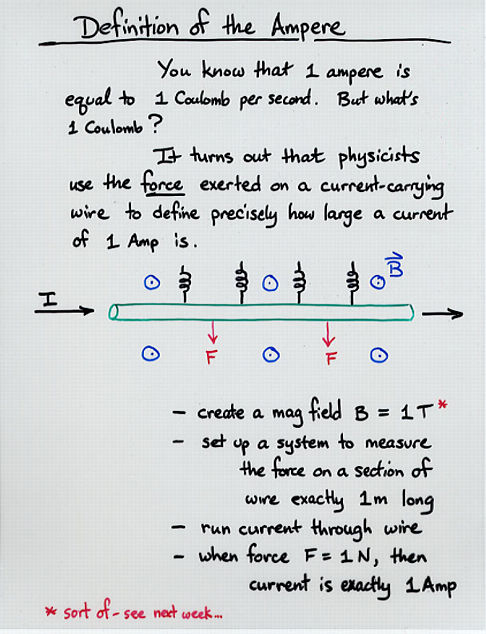Viewgraph 12