Magnetic Torques and Amp's Law

A magnetic field exerts a force on a straight wire carrying current; it exerts a torque on a loop of wire carrying current.
Torque causes an object to spin around a fixed axis.
Each loop of current has a direction associated with it: its normal vector is perpendicular to the loop, in the direction given by the right thumb when the right fingers curl in the direction of the current.
A magnetic field exerts a torque which tries to align the normal vector of a loop of current with the magnetic field.
The size of the torque on a loop of current is
```
       torque = (# turns) * (current) * (loop area) * (mag field) * sin(theta)
```
where theta is the angle between the magnetic field and the loop's normal vector.
A loop carrying direct current will not keep spinning in a constant magnetic field; it will instead just wobble back and forth. DC motors must use a split-ring commutator to permit them to spin fully around.
It is possible to create a magnetic field by running a current through a wire -- showing the close relationship between electricity and magnetism.
Ampere's Law permits one to calculate the strength of a magnetic field created by current in several simple situations.

The strength of a magnetic field around a long, straight wire is

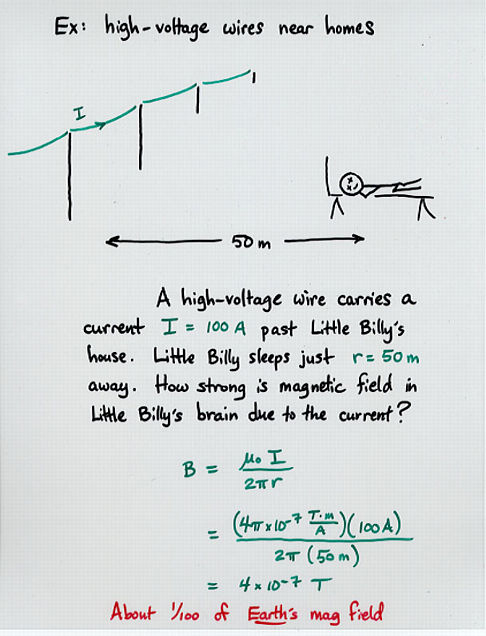
                         mu * current 
           mag field =  -------------------
                         2 * pi * distance

where mu is the magnetic permeability of free space:

              mu     =  4 * pi * 10^(-7)  T*m/A

                     =  1.257 x 10^(-6)   T*m/A

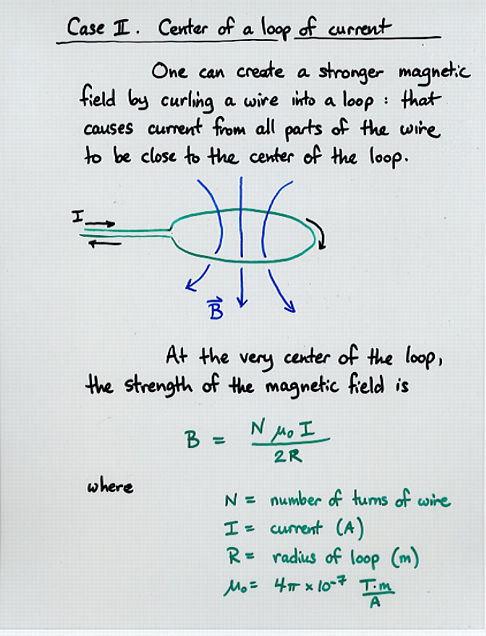
The strength of a magnetic field at the center of a loop of wire is

                         N * mu * current 
           mag field =  -----------------
                          2 * radius

where N is the number of turns of wire in the loop.

Viewgraph 1

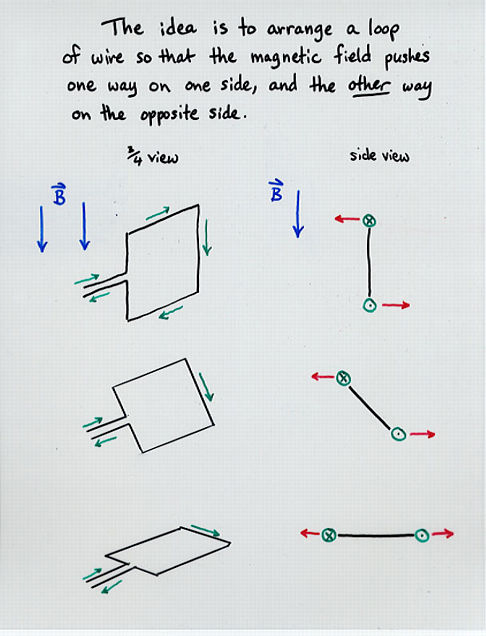Viewgraph 2

Viewgraph 3

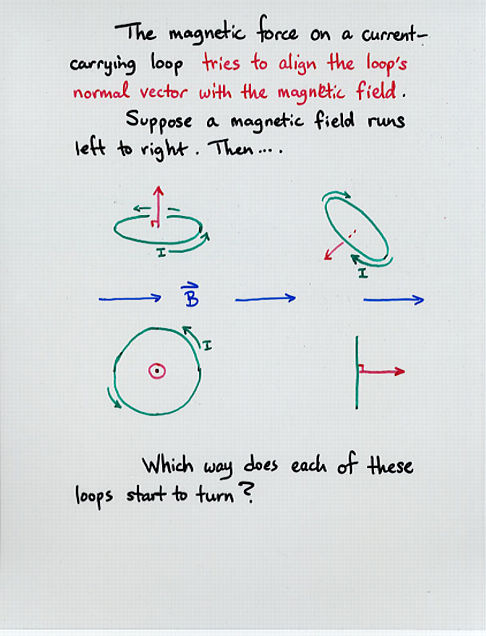Viewgraph 4

Viewgraph 5

Viewgraph 6

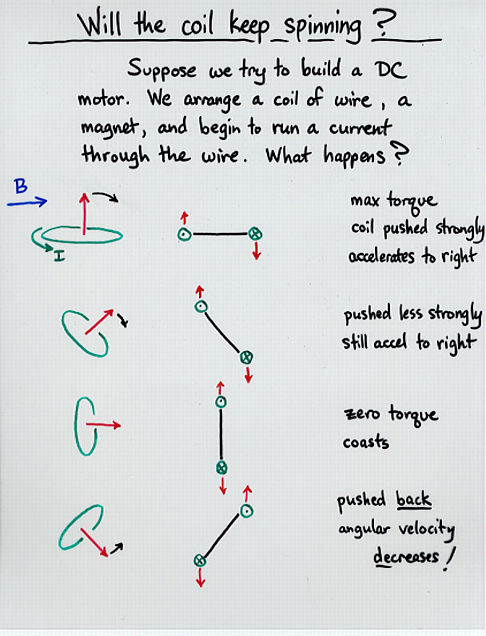Viewgraph 7

Viewgraph 8

Viewgraph 9

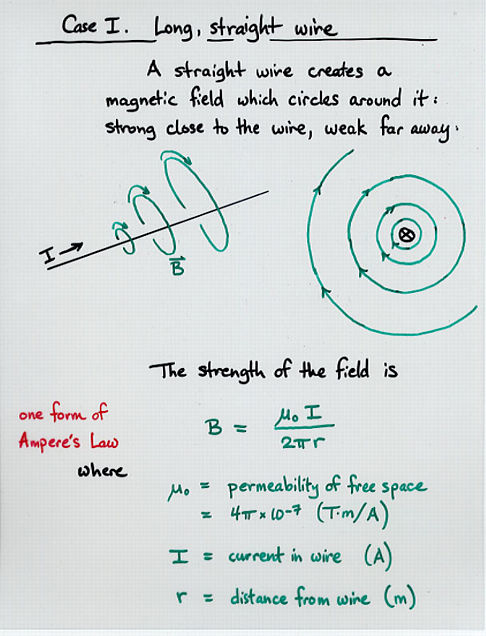Viewgraph 10

Viewgraph 11

Viewgraph 12

Viewgraph 13

Viewgraph 14