 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Show all work -- you may receive partial credit!
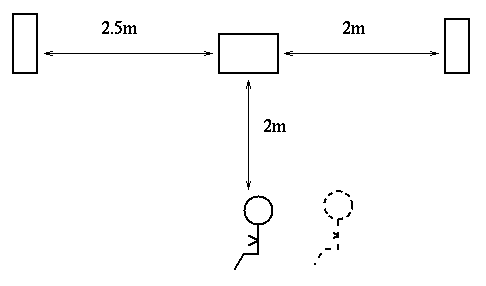
Joe unpacks his stereo system. He places the amplifier on his table, one speaker 2.5 m to its left, and the other speaker 2.0 m to its right. Joe then sits in a chair, 2.0 m in front of the amplifier.
Question 1: Draw a picture showing a view from above of Joe, the amplifier, and both speakers.

Question 2: What is the distance from Joe to the left-hand speaker, and from Joe to the right-hand speaker?
Answer: distance Joe to left speaker is
d(left) = sqrt( [2m]^2 + [2.5m]^2 ) = 3.20 m
distance Joe to right speaker is
d(right) = sqrt( [2m]^2 + [2m]^2 ) = 2.83 m
Assume that sound travels at v = 343 m/s. The speakers play a note with frequency f = 463.5 Hz.
Question 3: Does Joe hear constructive or destructive interference? Why?
Answer: the wavelength of this sound is
v 343 m/s
lambda = --- = -------- = 0.740 m
f 463.5 Hz
The difference in path length from Joe to the two speakers is
d(left) - d(right) = 3.20 m - 2.83 m = 0.37 m
= lamba / 2
Since the difference in path length is 1/2 of a wavelength,
the interference will be destructive.
Joe moves his chair sideways 0.25 m to the right.
Question 4: What sort of interference does he now hear? Why?
Answer: at his new position (dashed figure in diagram), Joe is at a distance
d(left) = sqrt( [2m]^2 + [2.75m]^2 ) = 3.40 m
d(right) = sqrt( [2m]^2 + [1.75m]^2 ) = 2.66 m
So the difference in path length now is
d(left) - d(right) = 3.40 m - 2.66 m = 0.74 m
Since the difference is exactly 1 wavelength, the two waves
interfere constructively.
This page maintained by Michael Richmond. Last modified Feb 26, 1997.
 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.