

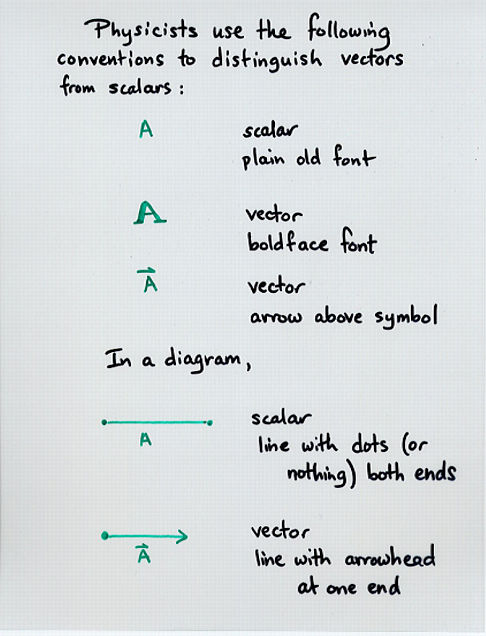

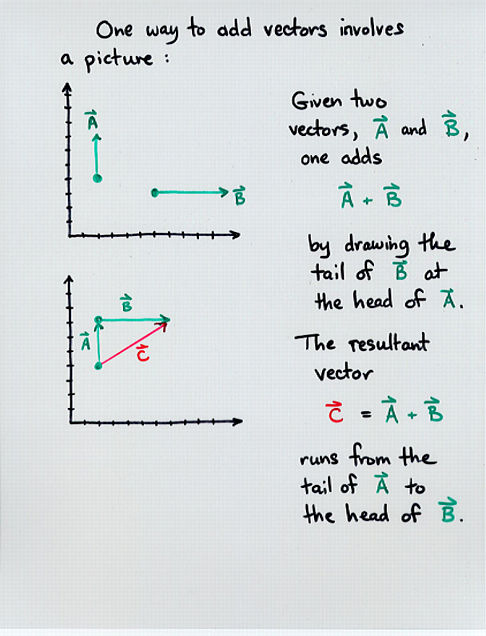
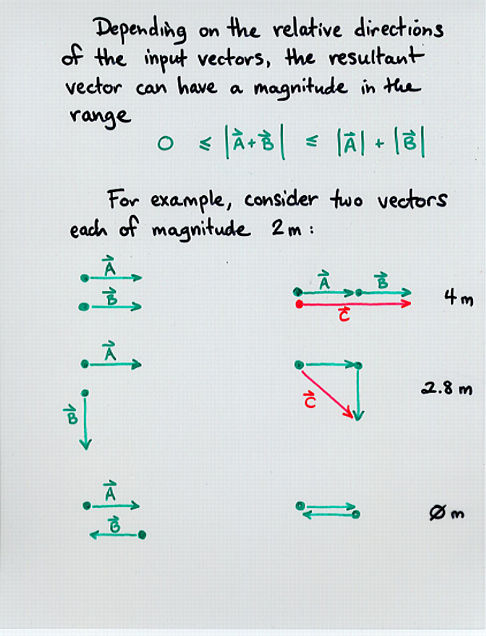
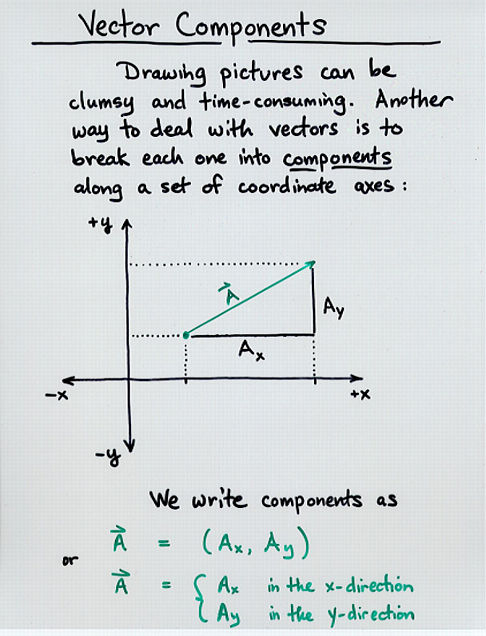


 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
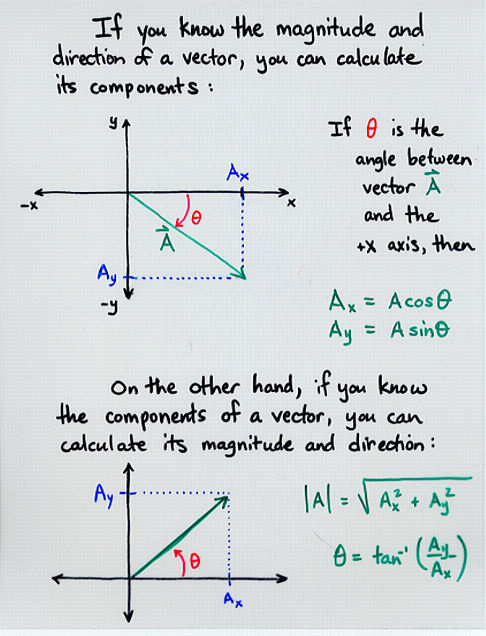
vector A = ( Ax , Ay )
vector A = ( 12, 5 )
vector B = ( -4, 20 )
x component y component
--------------------------------------
A + B 12 + (-4) 5 + 20
8 25
vector (A+B) = ( 8, 25 )
Viewgraphs










 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.