






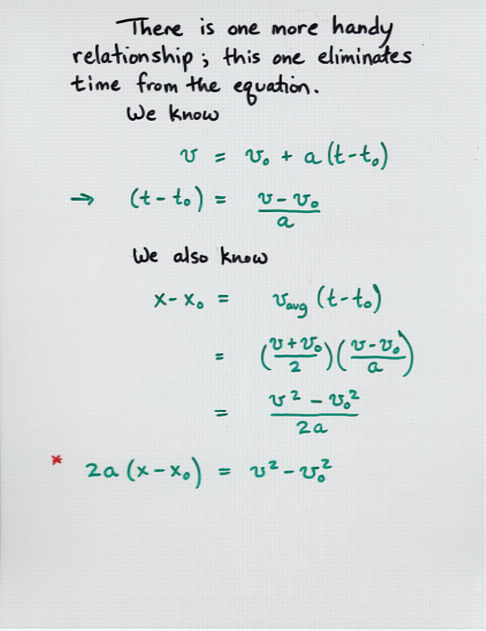





 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
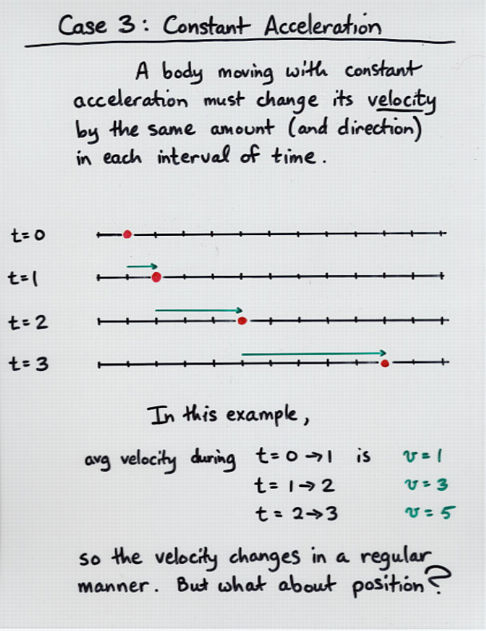
(x - xo) = v * (t - to)
(v - vo) = a * (t - to)
(x - xo) = (avg v) * (t - to)
1 2
(x - xo) = vo * (t - to) + --- * a * (t - to)
2
2 2
2 * a * (x - xo) = v - vo
v = a * t
x = (avg v) * t
1 2
x = vo * t + --- * a * t
2
2 2
2 * a * x = v - vo
Viewgraphs








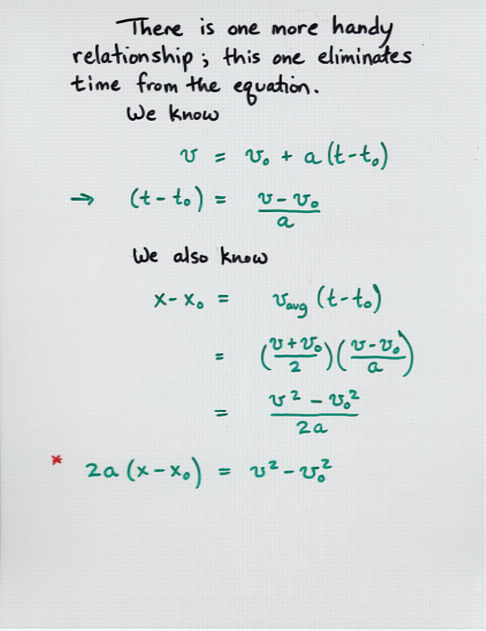





 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.