The Luge track

At the 2010 Vancouver games, competitors are sliding down a track built in Whistler, British Columbia. Click on the photo for a picture showing the track's path clearly.

Some details of the luge course on this track (I've made a few approximations, since the best numbers refer to the bobsled course).

Length:           1,374 m
Finish Altitude:    786 m
Start Altitude:     929 m
Number of Curves:    16

Suppose that an athlete of mass 70 kg slides down the track on top of his sled of mass 23 kg.

1. Under ideal conditions, what is the maximum speed this rider could reach at the end of the track?
2. How much work does gravity do on the rider+sled during the race?
3. The actual top speed of the sleds at the bottom of the course is about v = 40 m/s. How much work has friction done on the rider+sled?
4. Estimate the coefficient of kinetic friction between sled and ice.

Here is a closeup of the final turn:

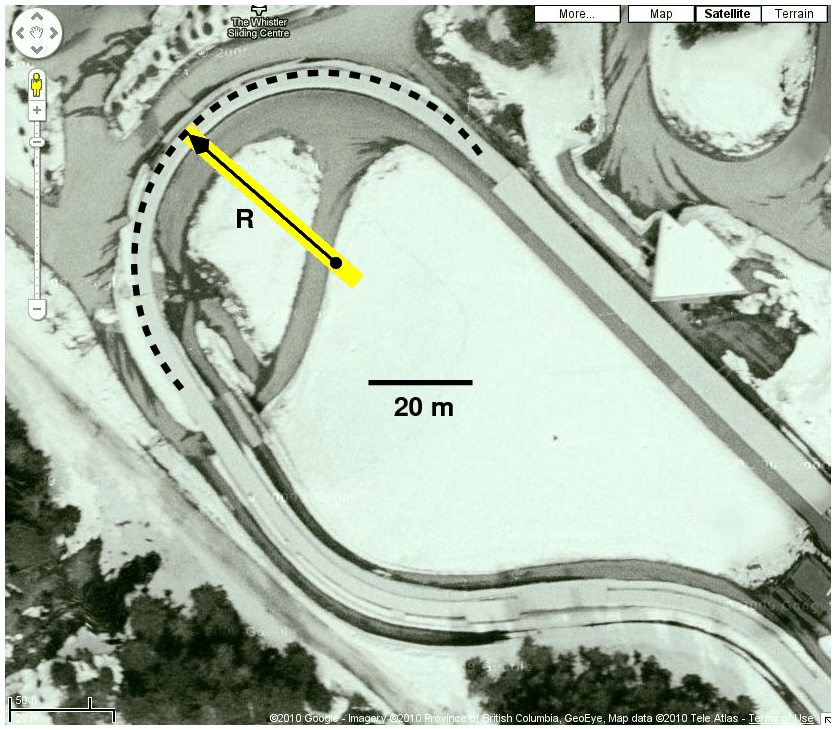
5. Suppose the actual speed at the finish line is about 40 m/s. When a sled moving at that speed goes around the final turn, what is its centripetal acceleration? Express your answer in m/s^2 and in gees.
6. What is the angular speed of the rider through this turn? Provide a magnitude, direction, and units.
7. What is the torque exerted on the rider+sled, measured around the center of the turn, as they zoom around? Provide a magnitude, direction, and units.

For more information

• Whistler's bobsled/luge course is fast -- and scary.
• Training at the Whistler Sledding Center
• Wikipedia's entry on the Whistler Sliding Center

Copyright © Michael Richmond. This work is licensed under a Creative Commons License.