Creative Commons License Copyright © Michael Richmond. This work is licensed under a Creative Commons License.

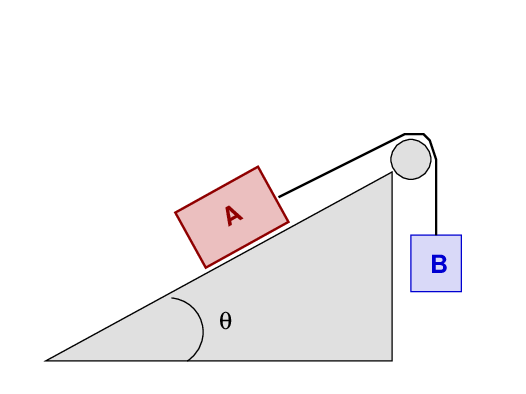
A tilted Atwood machine ... with friction!

Suppose that we create a modified Atwood machine, with a cart A sliding on a track, connected by a string to a weight B hanging in mid-air. We know the masses of the two objects, mA and mB, as well as the angle of the ramp θ,

But this time -- let's add one more complication: friction between the cart A and the ramp, with coefficients

Suppose that we hold both cart and weight fixed in place, and then release them. What will happen?

To find out, we must draw a free-body diagram for each object. First, the cart:

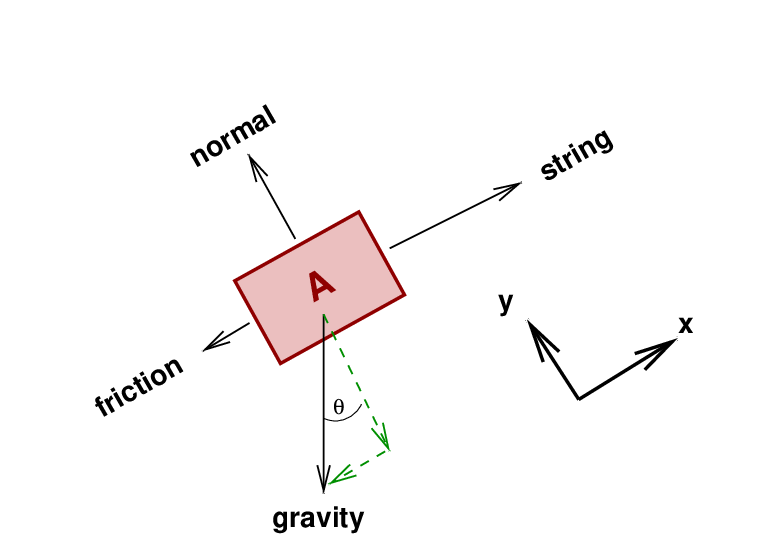
Let's assume that the cart is being pulled up the ramp by the string. In that case, the forces on the cart in the X and Y directions yield the following two equations:

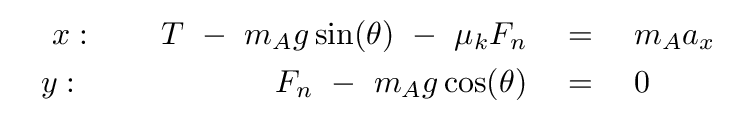
The Y-equation allows us to determine the size of the normal force on the cart.

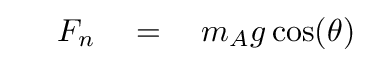
If we substitute this into the X-equation, we find

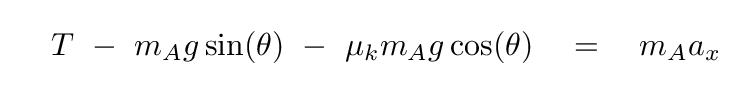
Hmmm. This is a single equation with two unknowns: the tension T and the acceleration of the cart ax. It's not possible to solve for the acceleration yet -- we need more information.

So, let's look at the forces on the weight. Remember, we are assuming that the cart rolls up the ramp, so the weight must be accelerating in the negative y-direction.

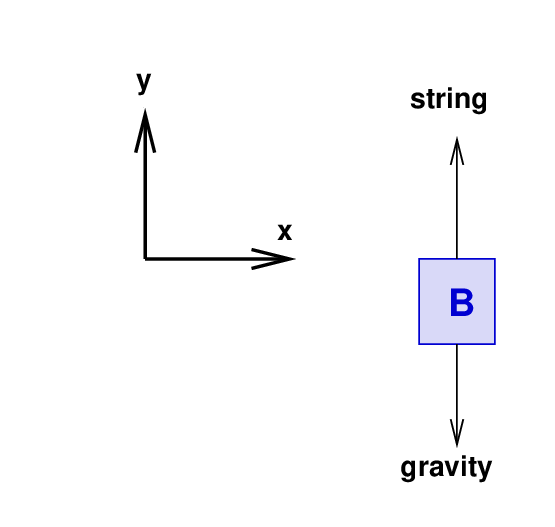
Newton's Second Law in each direction yields

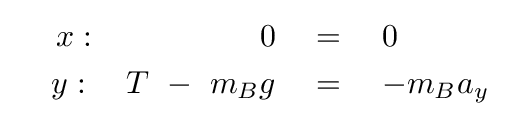
We can solve for T.

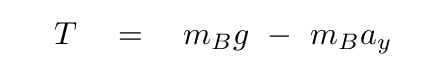
Now, since the cart is tied to the weight, their accelerations must be the same in size. In other words, we can replace the separate variables ax and ay with the single variable a.

If we substitute the tension force we derived from the weight's motion into the big equation for the cart, we end up with

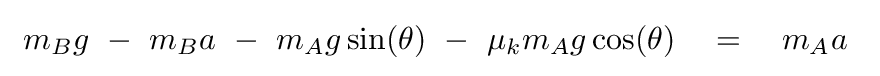
At this point, a bit of algebra will allow one to solve for the acceleration of the objects. Can you do it? 



  Q:  Suppose that 

          mass of cart   mA  = 4.0 kg
          mass of weight mB  = 3.0 kg
          angle of ramp  θ   = 35 degrees
          coeff of fric  μk  = 0.10

      Which way does the cart move?  How large is its acceleration?

My answer. 



  Q:  Suppose that 

          mass of cart   mA  = 6.0 kg
          mass of weight mB  = 1.0 kg
          angle of ramp  θ   = 25 degrees
          coeff of fric  μk  = 0.20

      Which way does the cart move?  How large is its acceleration?

My answer.

Creative Commons License Copyright © Michael Richmond. This work is licensed under a Creative Commons License.