Torque with vectors

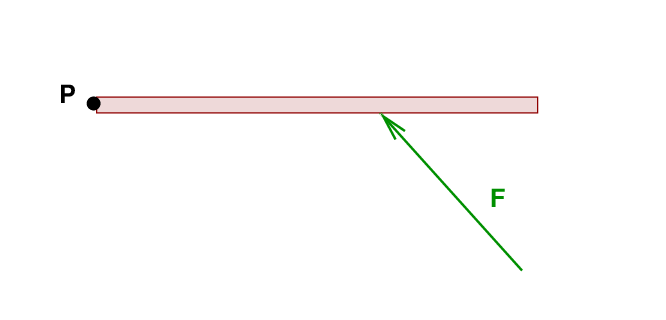
Just a few days ago, we learned about torque: the rotational analog of force. The torque exerted by a force around some pivot point depends on a number of factors. Consider the situation below:



  Q:  How can we compute the torque produced by the
          force F around the point P?

Right. First, we determine the radius vector r, from the pivot to the point at which the force is applied.

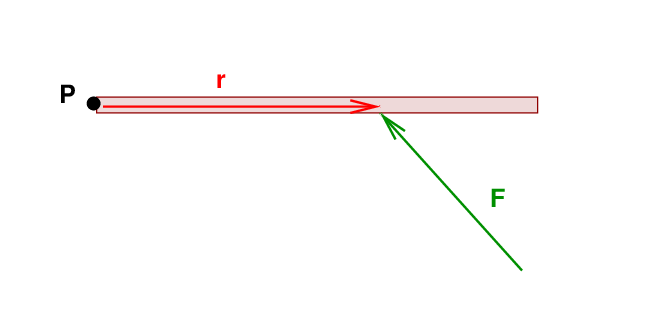
Once we know both the radius and force vectors, we draw them tail-to-tail and measure the angle between them.

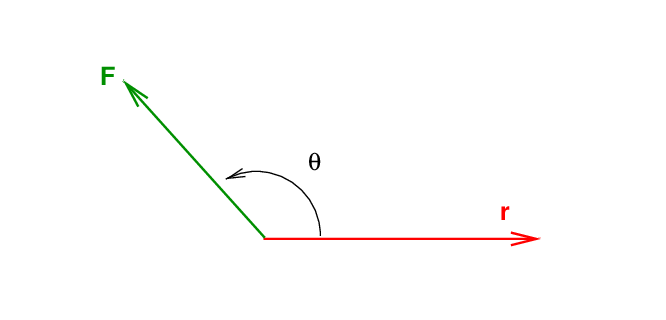
The magnitude of the torque is then given by

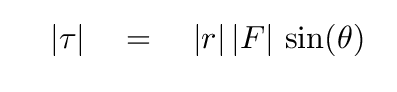
The direction of the torque is given by this version of the right-hand-rule:

raise your right hand
point your fingers in the direction of the radius vector
orient your hand so that you can curl your fingers in the direction of the force -- without breaking your fingers!
now stick out your right thumb. It points in the direction of the torque

But -- what if we aren't given a nice picture or diagram showing all the objects and forces? Suppose that instead, we are given both the radius r and force F as VECTORS.

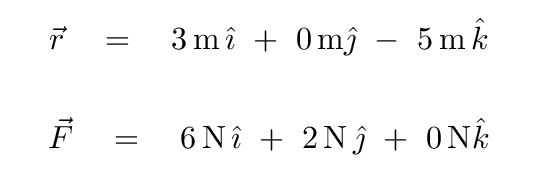
In order to compute the torque produced by these inputs, we need to turn to a new mathematical tool: the cross product.

Mathematics of the cross product

Now that we know how to perform the cross product, we can apply it to some physics problems.

Some examples of torque in action