Standing waves on a string experiment

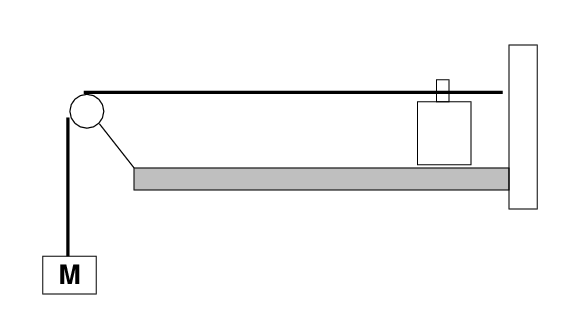
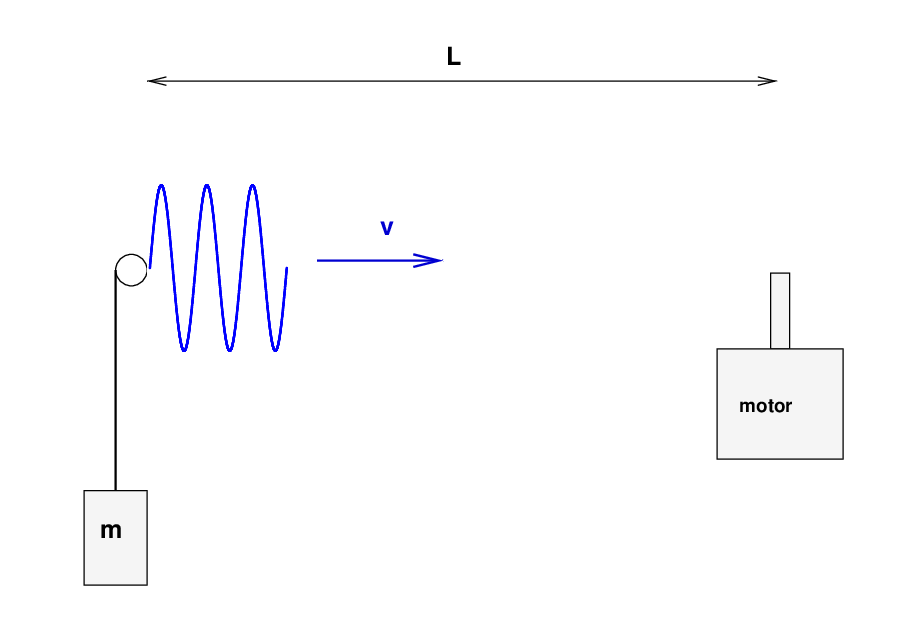
At the front of the room is a device similar to that shown in the diagram above. It consists of

a piece of thick white string
a mass hanging from the string, which puts the string under TENSION
a small motor which pushes the string with a periodic force
a dial that controls the FREQUENCY of the motor

If we set the frequency of the motor to some random value, then even though it pushes and pulls the string, there is very little apparent motion.



   

      Watch as a random frequency leads to ... not much

But if we choose just the right frequency, we can cause the string to oscillate up-and-down with a considerable amplitude.



   

      Watch as one particular frequency leads to big oscillations

The questions are --- why do some frequencies create big oscillations? and just what are those special frequencies?

I'll answer the first question, but you will have to answer the second.

Why do some frequencies lead to big oscillations?

Let's begin with the motor turned off, so that the string is motionless -- though it does remain under tension T. The length of the string, from the motor to the pulley, is L.

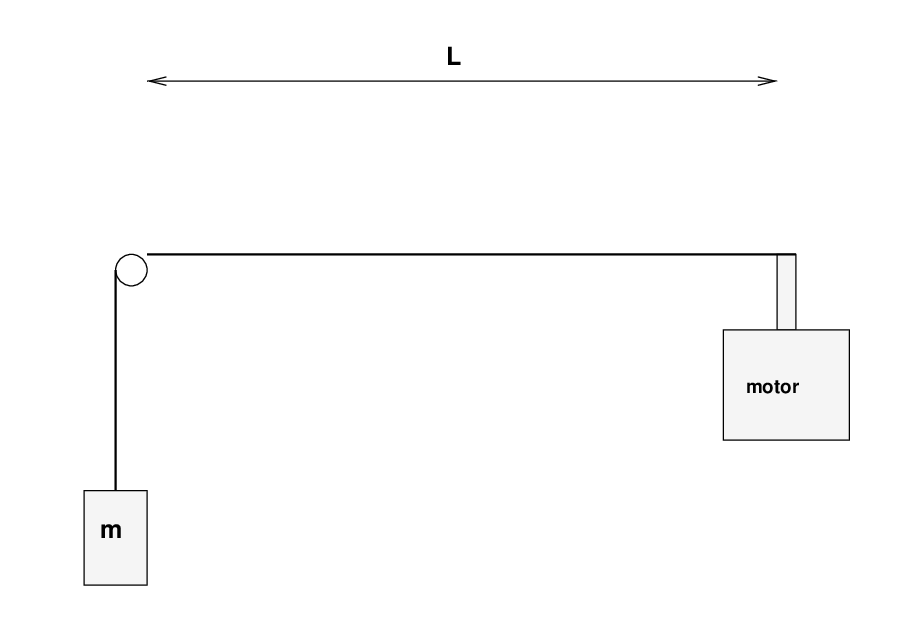
Now, at time t = 0, we turn on the motor. It starts to move up and down with frequency f. The period of oscillation is

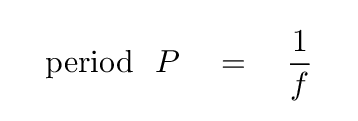
The small rod attached to the motor pushes the string as it moves up and down, creating a disturbance that starts moving to the left.

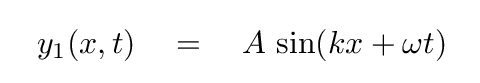
This wave will take a time

When the wave reaches the pulley, it bounces off and sends a reflected version of the wave travelling back toward the motor.

Since the reflected wave is a copy of the original wave, this trip also takes

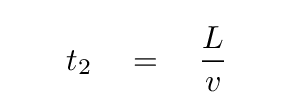
As a result, the reflected wave will return to the motor after a time

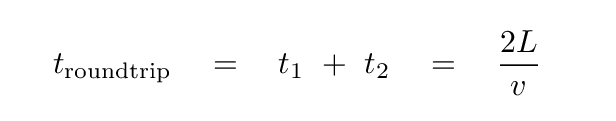
As the waves created by the motor travel to the left, and the reflected waves travel back to the right, they will pass through each other.

If -- and this is a big if -- we choose just the right frequency, then the two waves will add together to form a standing wave with a large amplitude.

So, what's the big secret? What is the reason that some frequencies will create standing waves, but most will not?



   A standing wave will form if the reflected wave returns
        to the motor after just as the motor is starting
        another cycle.  In other words, 

   the wave must make one round-trip journey in exactly one period, 
        or two periods, or 3 periods
        or ... N periods.

In this setup, the length L of the string is fixed. I'll write it on the board in class. In order to find the special frequencies which will give rise to standing waves, there's one more piece of information we need: the speed of waves travelling on the string. We could compute the speed via

if we knew the tension T and linear mass density μ.

You must do the following in your report

Your job: perform the work described below, scan all work and pictures if necessary, and submit a single PDF to myCourses assignment "Standing Waves on a String

Look at the hanging mass to figure out the tension in the string
Measure the properties of the piece of cord on your desk in order to calculate the not-under-tension μ₀
Use the following measurements of the string at the front of the room to figure out how that density will change when the string is put under tension
```
              length of string not under tension   L₀ = 1.09 m
              length of string under tension       L  = 1.64 m

        
```
Write down your calculations showing the tension T
Write down your calculations showing the linear mass density under tension μ
Compute the velocity v of waves on the string under tension

Okay! Now that you know the speed v, you can start finding those special frequencies which will yield standing waves.



Number of periods      Frequency (Hz)         Wavelength (m)
        N                      f                    λ
-----------------------------------------------------------------------

        1

        2

        3

        4

-----------------------------------------------------------------------

Finally, for each of these frequencies, draw a picture showing the position of the string when the oscillations are at their maximum amplitude. Note that the string is held at end end, which means that it cannot move at both ends.

Write out the answers to all questions, draw all pictures, then scan everything. Submit a single PDF to

myCourses assignment "Standing Waves on a String