Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Black holes (the sort we will discuss here, anyway) are the remnants of stars which were originally much larger and more massive than our own Sun. When such stars run out of nuclear fuel in their cores, they can collapse in on themselves due to the relentless pull of gravity.
All we need to know about these black holes is that they are
In some very rare circumstances, two massive stars which were born from the same cloud of gas and dust, and orbited each other for millions of years, may both turn into black holes. If that happens, then the two black holes will continue to orbit around each other.
But something VERY interesting happens over time. The intense gravitational field of the black holes warps space-time around the pair, and some of their energy and angular momentum is radiated away in the form of gravitational waves. As the binary loses energy, the orbit shrinks, and the stars move closer together; but, as the orbit shrinks,
Image and video courtesy of
Georgia Tech / LIGO / T. Pyle
The result is an accelerating MERGER of the two black holes, leaving just a single black hole with the sum of the masses of the two original black holes (well, minus some mass which was turned into gravitational waves and radiated away).
So, if we had some way to detect gravitational waves, we might expect that our "gravitational wave telescope" would occasionally see a source of waves which grew stronger, and oscillated faster, and grew stronger, and oscillated faster -- and finally disappeared (because a single, isolated black hole will not create waves in the space around it).
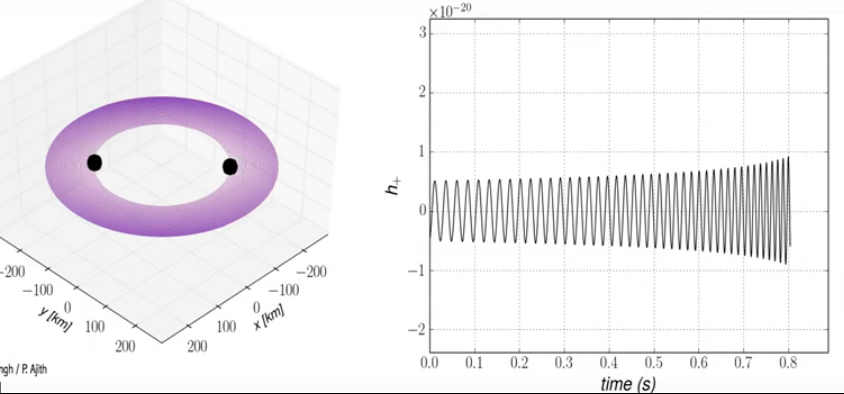
Image and video courtesy of
Sounds of Spacetime
You can play
this sound file
to "hear" the change in the frequency of the gravitational waves.
Play the video at 2x speed, and start the audio at 0:18 into the video
That's the theory -- but how can one detect gravitational waves?
How can one detect any gravitational wave, big or small?
The answer is based on the way that a passing gravitational wave will interact with space and matter. As a wave flies through some region of space, it causes space to contract in one perpendicular direction (and expand in the other), and then expand in that perpendicular direction (while contracting in the other).
For example, if we put this portrait on the wall, and then send a gravitational wave flying into the wall, we would see it distort as ... (click on the image).
One way to detect such a wave is to use an interferometer with two long arms. Light waves from a single laser are split, so that half run down one arm and half run down the other. After bouncing off mirrors at the end of each arm, the two beams are combined at a sensor.
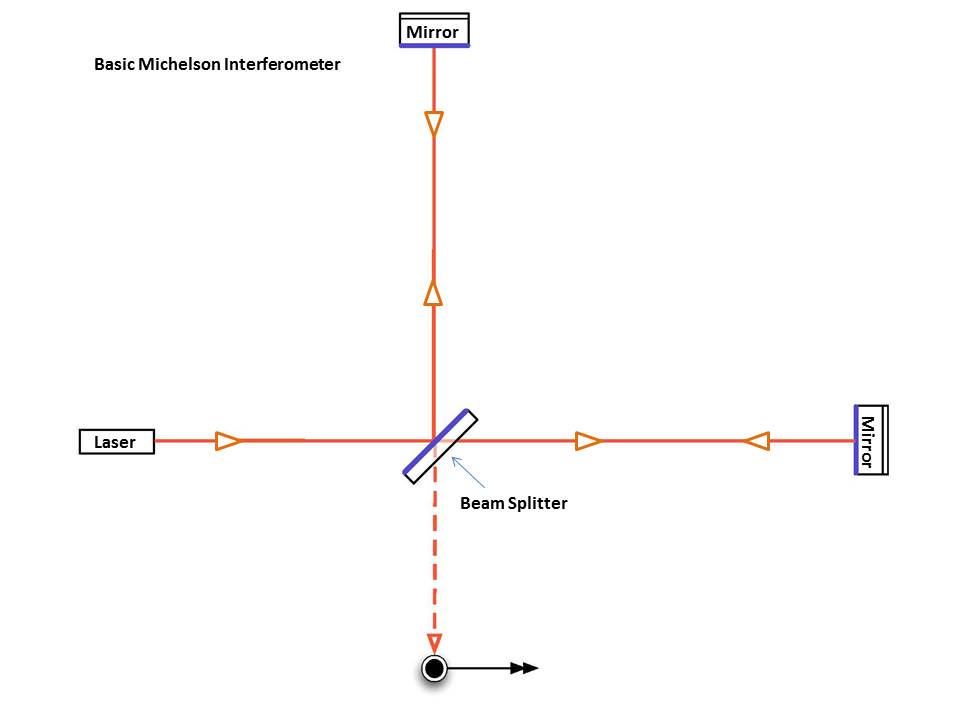
Image courtesy of
LIGO
We can adjust the length of the arms so that -- when no gravitational waves are present -- the two beams combine DESTRUCTIVELY, yielding a big fat "nothing" at the sensor.
Q: How should can we make the two light waves interfere
in a DESTRUCTIVE manner?
Q: How should we arrange the lengths of the two arms,
L1 and L2, so that the light waves interfere
in a DESTRUCTIVE manner?
Right. The key is to make the distance that one light wave travels exactly one-half of a wavelength longer than the distance the other light-wave travels. Or three-halves of a wavelength, or five-halves, or ...
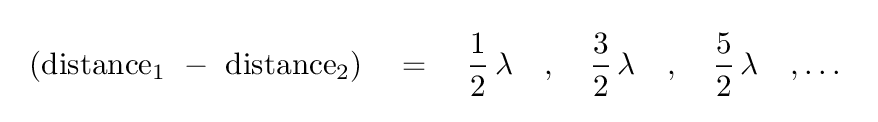
And that means the lengths of the two arms should be
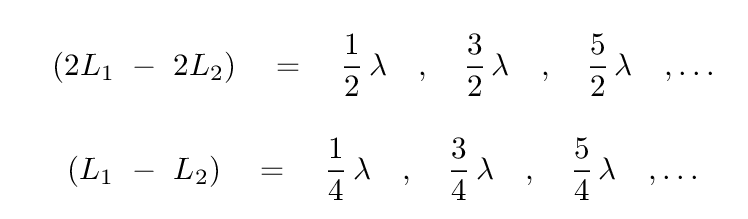
So, if we set up our interferometer so that there is perfect destructive interference under ordinary circumstances, then when a gravitational wave happens to fly past us, it will modify the lengths of first one leg, then the other. That will cause the two waves to move out of perfectly destructive interference -- and so we should see a small amount of light when the two laser beams come back together. As the gravitational wave passes, the light should oscillate on and off, on and off, at the same rate that the two black holes orbit around each other.
Well, that's the basic idea, anyway. A real interferometer like LIGO is a bit more complicated. Okay, a LOT more complicated.
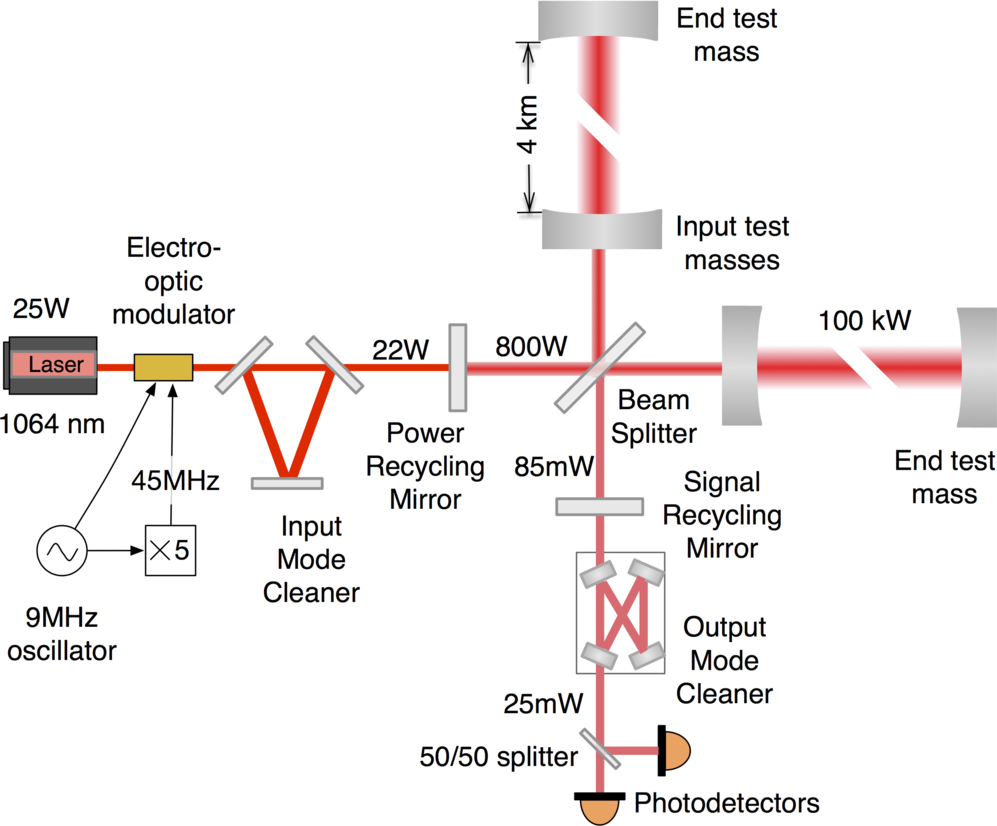
Image courtesy of
LIGO
But before we talk about the real LIGO any more, let's try to figure out one very important feature of an interferometer-type gravitational wave detector: how long should the legs be?
Well, if gravitational waves caused objects like pictures and cars and people to warp by the amount in my example, then it would be simple to detect them: just look with your eyes.
Unfortunately, the gravitational waves that reach us on Earth from very distant events are weak -- really weak. It turns out that in order to produce a change in the length of the two arms which is SOMEWHAT SMALLER THAN THE DIAMETER OF AN ATOMIC NUCLEUS, the arms need to be ... pretty long.
It turns out that the real LIGO has legs which are about L = 4000 m = 4 km long.
Image courtesy of
Caltech/MIT/LIGO Lab
Of course, it's a very complicated business, and a feat of engineering. For example, the light beams must travel through a vacuum to avoid scattering off air particles. So, each leg is a 4-km-long vacuum chamber:
Image courtesy of
Caltech/MIT/LIGO Lab
The mirrors must be protected from vibrations, so the engineers have created a very sophisticated apparatus for isolating them from disturbances. The mirror, of mass 40 kg, is the FOURTH in a series of pendula. The other objects in the chain have a total mass of about 320 kg; acting as a system, they damp out most of the vibrations and allow the mirror to hang freely.
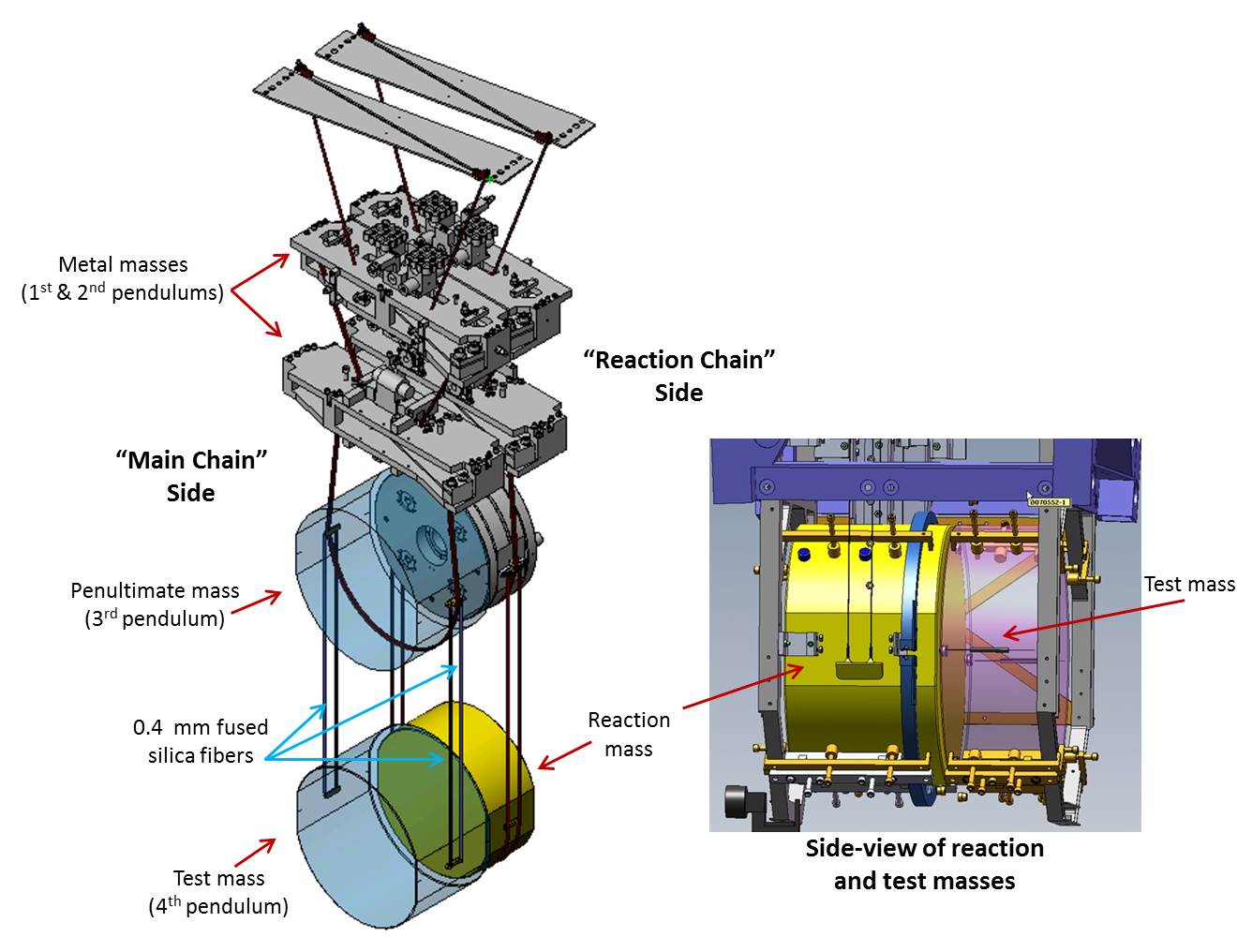
Image courtesy of
LIGO collaboration
Note the rather fragile-looking connection between each mirror and the fibers of the pendulum:
Image courtesy of
LIGO collaboration
Well, back in 2015, when LIGO reported its first detection of two black holes merging, the "chirp" signal it recorded looked (and sounded) like this:
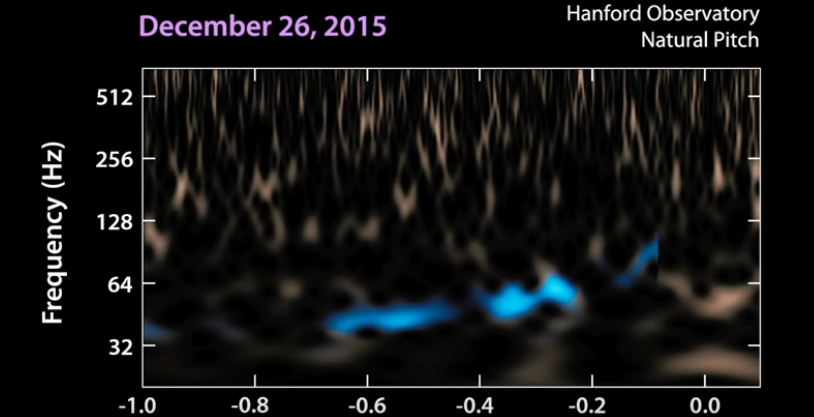
Image and video courtesy of
LIGO
Since 2015, LIGO and the other gravitational wave detector, VIRGO, have found a number of other merging systems. In most cases, the waves are produced by two black holes merging; but in a few, the objects are either two neutron stars, or a neutron star and a black hole. (The gravitational-wave detections in the picture below are the light-blue ones at the top, and the small number of orangey ones at the bottom).
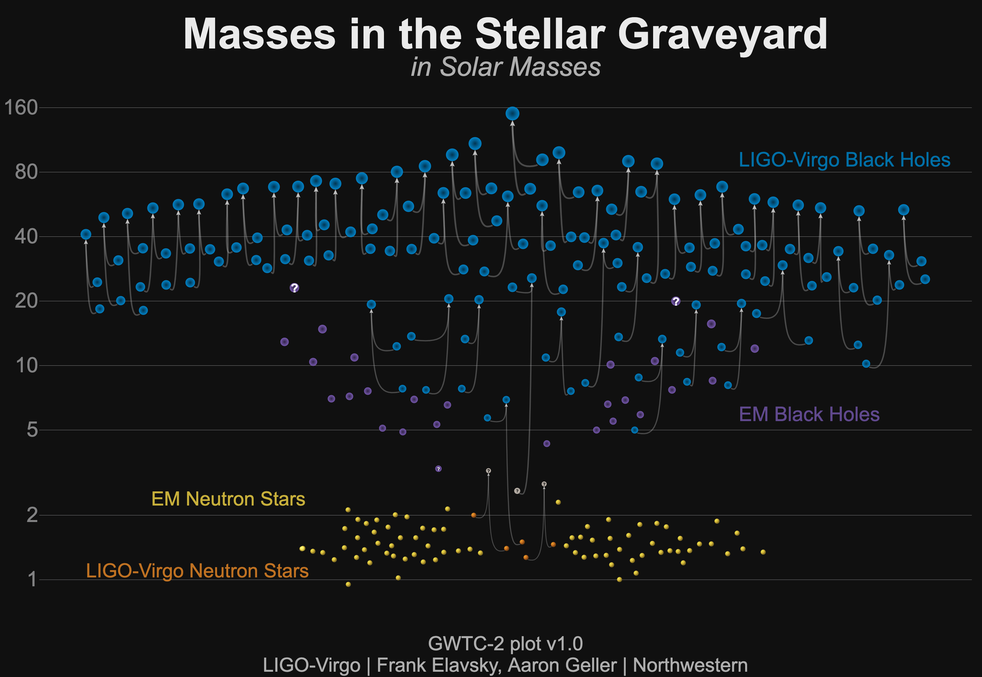
Image courtesy of
LIGO/VIrgo/Northwestern Univ./Frank Elavsky
Consider the case of GW170817, a binary-black hole merger detected in August, 2017. This was the first real event to be observed by three antennae: both LIGO sites, and the VIRGO detector near Pisa, Italy. The signal arrived first in Livingston, the 8 ms later in Hanford, and 14 ms later in VIRGO.
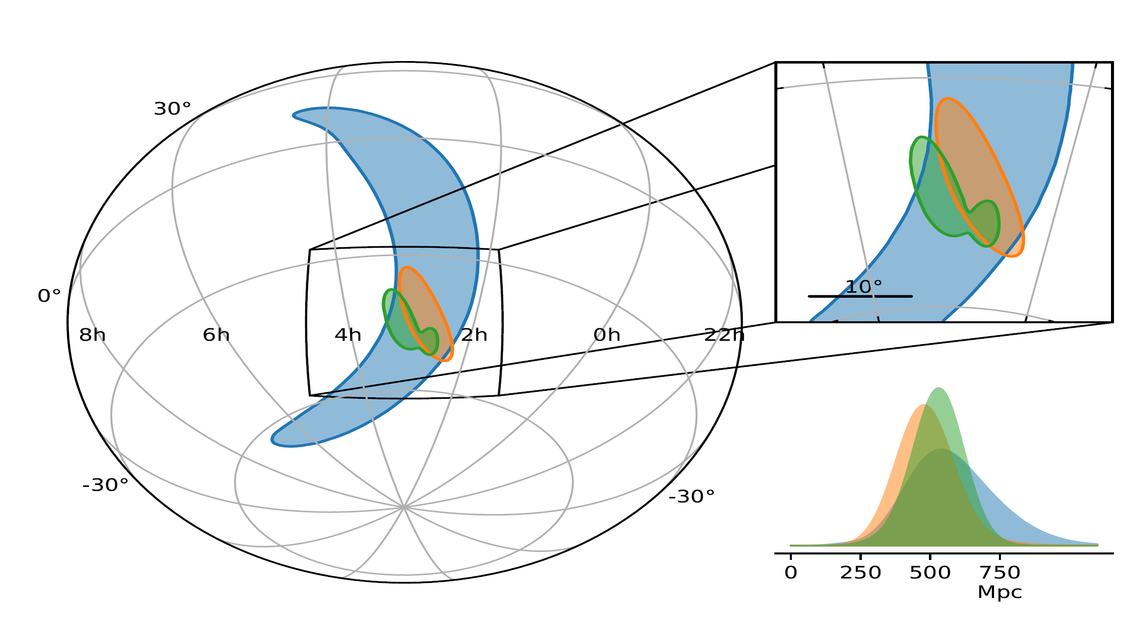
Figure 3 taken from
LIGO's index of GW170814 publications
The figure below shows the localizations of some the current gravitational wave detections; most were made only by the two LIGO antennae, but the two most recent, GW 170814 and GW170817, include VIRGO as well. Note how much smaller they are.
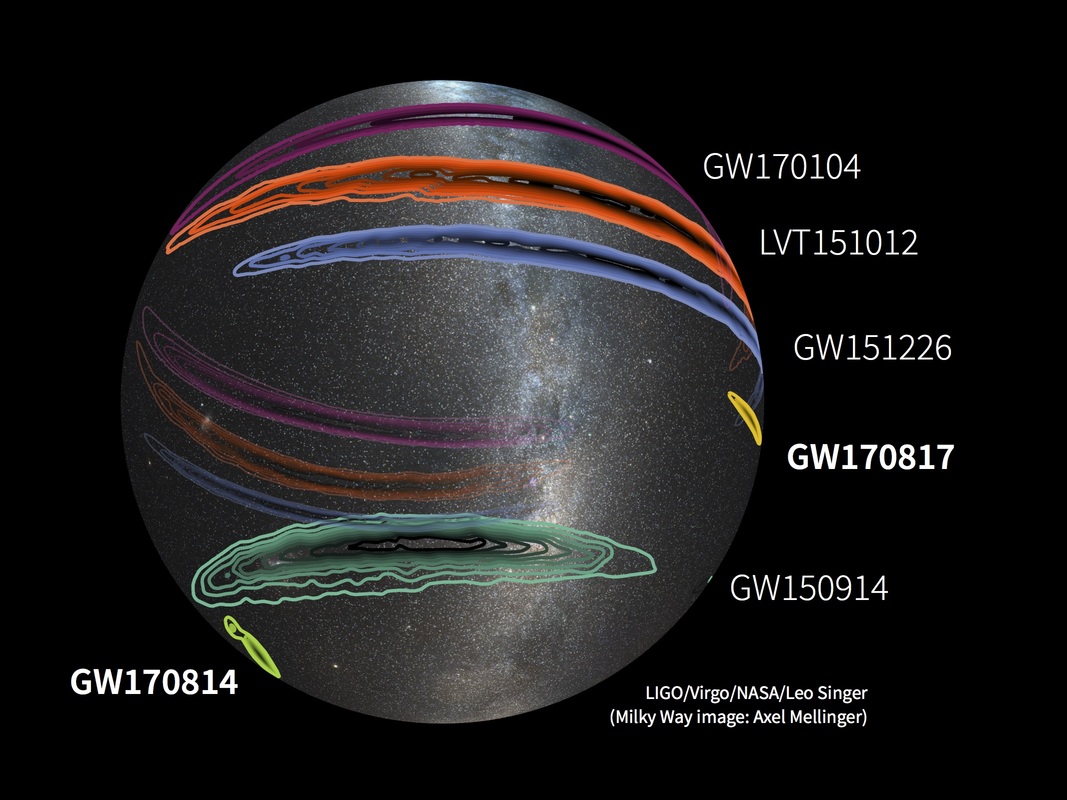
Figure courtesy of
LIGO/Virgo/NASA/Leo Singer
GW170817 was a merger of neutron stars, producing a counterpart in electromagnetic radiation. The combined LIGO Hanford + LIGO Livingston + Virgo localization yielded a relatively small region for optical (and radio, and X-ray) astronomers to search.
Image courtesy of
LIGO's GW170817 information page;
LIGO/Virgo/NASA/Leo Singer
As a result of this relatively small search area, astronomers were able to pin down the position of the counterpart within less than one day from the detection of the gravitational wave. In the figure below, the short vertical dashes represent the times when information was reported via GCN Circular.
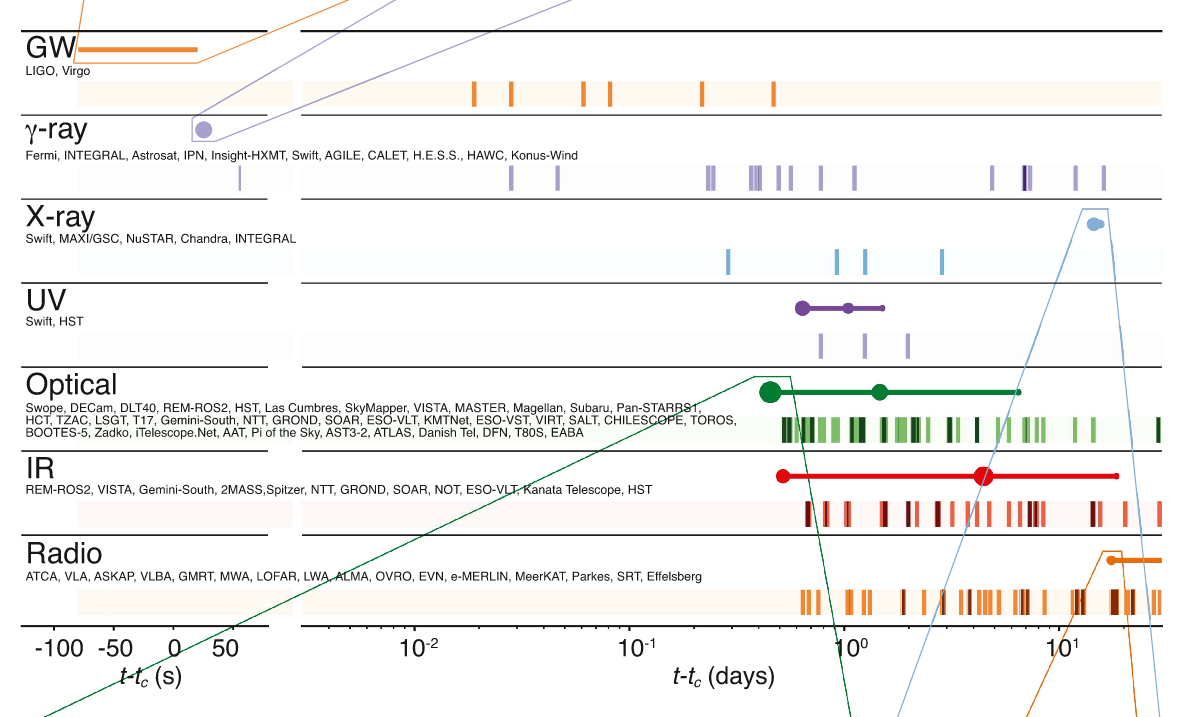
Taken from Figure 2 of
Abbott et al., ApJL 848, 12 (2017)
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.