
 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Why does a ball roll down a hill? One way to answer the question is to look at the torque on the ball as it sits on a slope. Consider this hollow ball rolling down a ramp:

Gravity exerts a force F = mg on the center of the ball, directed vertically downwards. Now, if the ball is rolling without slipping, that means that the portion of the ball which touches the ramp is -- for a moment -- motionless. The ball rotates around this point of contact.

Therefore, we can look at the torque exerted around this point of contact by the force of gravity. Let's zoom in ...
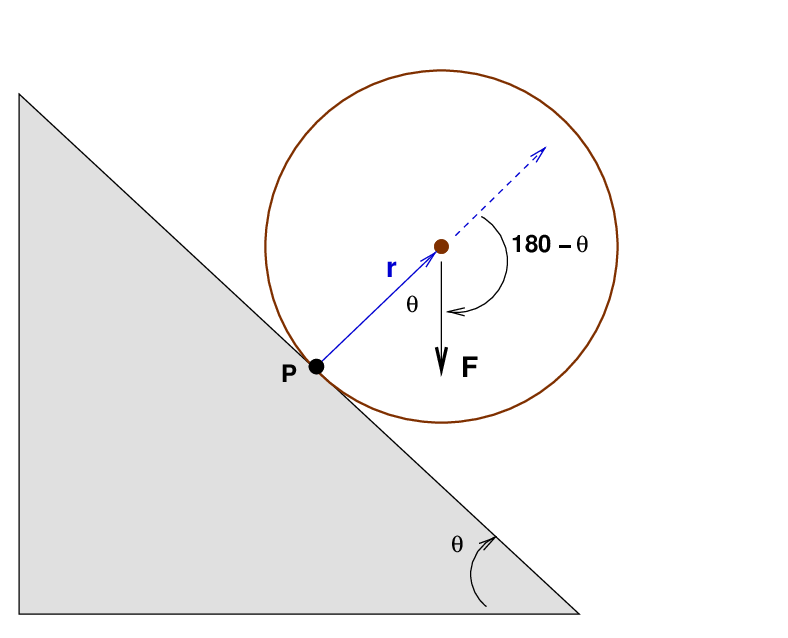
Q: What is the torque around P, the point of contact?
Provide both a magnitude and a direction.
My answer.
Q: Express this torque in terms of the mass of the
ball, M, and the radius of the ball, R.
My answer.
Q: What is the moment of inertia of the hollow ball around its
center of mass?
My answer.
Q: What is the moment of inertia of the ball around its
the point of contact with the ramp?
My answer.
Now, how does the ball respond to this torque? Well, it has some moment of inertia, I, so the torque causes it to change its angular velocity. In fact, the angular acceleration must be

Q: Place the expression you derived for the magnitude
of the torque in the top of this equation, and
insert the moment of inertia around the point of contact in
the bottom of the expression.
What is the angular acceleration?
My answer.
Q: Convert the angular acceleration to a linear acceleration.
My answer.
Q: If the ball starts at rest at the top of the ramp, what will
its linear velocity be when it reaches the bottom of the ramp?
Express the velocity in terms of the ramp's height h.
My answer.
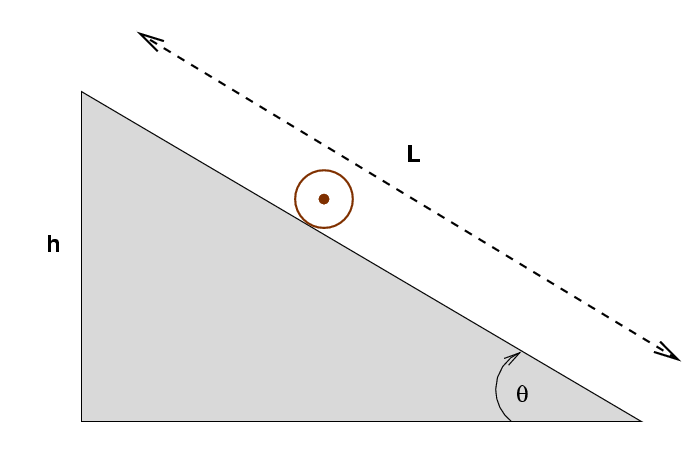
One last question. We've calculated the linear acceleration a of the ball, which turns out to be a constant value; it doesn't change as the ball rolls down the ramp. We also know the length L of the ramp. That means we should be able to use the good old equations of 1-D kinematics to figure out how long it takes the ball to roll all the way down to the bottom.
Q: How long will it take the ball to roll down
this ramp?
We can start with the kinematic equation, inserting our value for linear acceleration a.
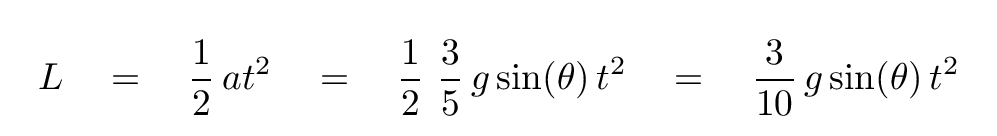
Recall that the sine of the angle of the ramp is just its height divided by its length (along the tilted surface). We can therefore replace the sin(θ) term with h/L.
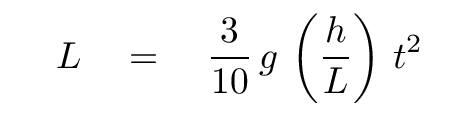
Solving for the time to roll down the ramp, we end up with a time that depends only on L, g, and h.
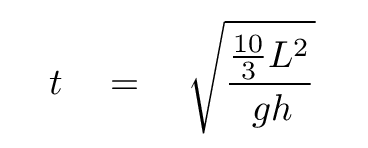
 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.