Creative Commons License Copyright © Michael Richmond. This work is licensed under a Creative Commons License.

Classwide pendulum experiment -- what is the value of "g"?

What is the value of g? You may think it is 9.8 m/s2, or maybe 9.81 m/s2; but the actual value depends on a number of factors. The latitude at which the measurements are made affects the value, as does the altitude, and even local topography. The differences are small, but they can be detected with a very careful experiment.

So, what's the local value of g in Rochester? Let's find out.

  1. Every pair of students in the classroom, or single student at home, will act as a "test unit."

  2. Each "test unit" will choose one length, somewhere between 0.10 and 2.0 meters. The rules are
    1. units with last names starting with A-F must choose between 0.10 and 0.30 meters
    2. units with last names starting with G-M must choose between 0.30 and 0.80 meters
    3. units with last names starting with N-R must choose between 0.80 and 1.20 meters
    4. units with last names starting with S-Z must choose between 1.20 and 2.00 meters
    (If you try and try and can't get a length in the range for your name to work, don't worry. Just pick a length which _will_ work for your setup, and report that)

  3. Each test unit will make 3 trials of a single length, measuring the time taken for 10 complete cycles. Divide this time by 10 to determine the period for one cycle.

  4. Compute the average period for the three trials, and the standard deviation.

  5. Place your values for length, average period, and standard deviation of period, into the YELLOW squares of the spreadsheet below

  6. (optional) If you have extra time, you can choose a second, different length, and make another set of measurements. If you do this, place these values into the GREEN squares in the spreadsheet, down below the yellow ones.

Once a large number of values have been entered into the spreadsheet, we will turn out attention to using this dataset to measure the local value of g. How?

Well, we know that the period of a pendulum is related to its length, and to g.

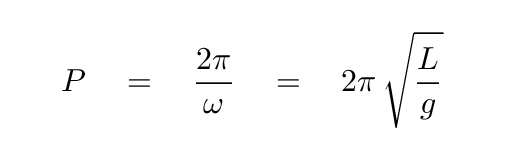
If one squares both sides of this equation, one will find

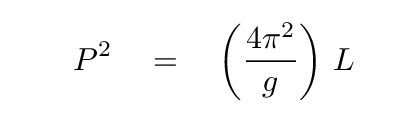
So, if we combine all our measurements onto a single graph, and we choose the axes of that graph properly ... then the slope of the line on that graph will be related to the local value of g.

Your job:

Make a copy of all the data from the class spreadsheet. Use it to create a graph in the format shown above. Determine the slope of the line which best fits the data, and estimate an uncertainty in that slope. Then use that slope (and uncertainty) to compute a value (and uncertainty) for g, the local acceleration due to gravity.

You must submit your graph, and your calculations of "g", into

Creative Commons License Copyright © Michael Richmond. This work is licensed under a Creative Commons License.