Tilting an Atwood machine

Suppose that we set up a modified Atwood machine -- one block on a track, one hanging in mid-air, tied together with an ideal string -- but we TILT the track.

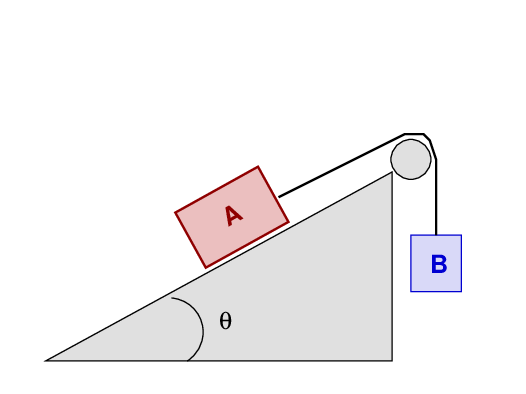
We hold both blocks motionless for a moment ... and then we release them. What is going to happen now? There are three possibilities:

1. the block B falls down, and drags the block A up the ramp
2. nothing moves
3. the block B slides down the ramp, and pulls block A upward

Which one will actually take place? That depends on the properties of the system. What are the masses of the two blocks? Is there any friction on the ramp?

Let's try a simple version -- no friction between ramp and block A. If you can answer these questions, you'll be able to determine which block (if any) moves downward, and the value of its acceleration.

• Using a coordinate system tilted to match the ramp, what is the net force on block A?
• Using a coordinate system which is not tilted, what is the net force on block B?
• The acceleration of the two blocks must be identical ... but their SIGNS must be opposite. Assume for a moment that the block B falls downward. Write two equations, using the same symbol a for both blocks. In other words, for block A, let a_x = a, and for block B, let a_y = -a
• Solve the two equations for the value of a.
• Now, interpret the result:
  • If a = 0, then nothing moves when released.
  • If a > 0, then block B accelerates downward, as assumed, and block A slides up the ramp
  • If a < 0, then block B accelerates UPWARD, opposite to our guess, and block A slides DOWN the ramp