Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
The moment of inertia of a basic shape, rotating around its center, can be found in a table of moments of inertia. That's easy.
But suppose an object with a basic shape is rotating around some OFF-CENTER point? The object below is a square plate of mass M and side length L.
In such a case, you can start with the moment of inertia of the shape, as if it were spinning around its center of mass, but then add an extra term that accounts for the off-center location of the rotation.
where
Q: What is the moment of inertia of the plate around its center? Q: What is the distance d?
Right.
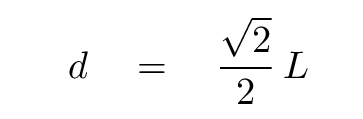
That means that when we put the pieces together, the moment of inertia of the plate rotating around point P is
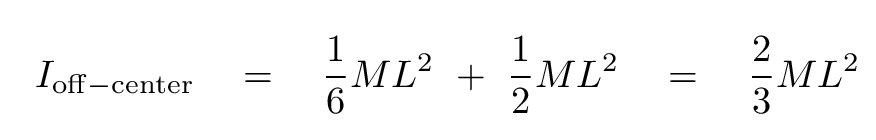
Okay, let's try this again. I'll create an object by connecting four meter sticks to create a square.
Each stick has
We rotate the object around the center of the square, marked with an "X" in the figure above.
Q: What is the moment of inertia of each stick around its own center?
Q: What is the distance from the center of each stick to
the axis of rotation?
Q: What is the moment of inertia of each stick around the center?
Q: What is the moment of inertia of the entire object?
One more example. This time, let's look at a barbell formed from two solid balls connected by a rod.
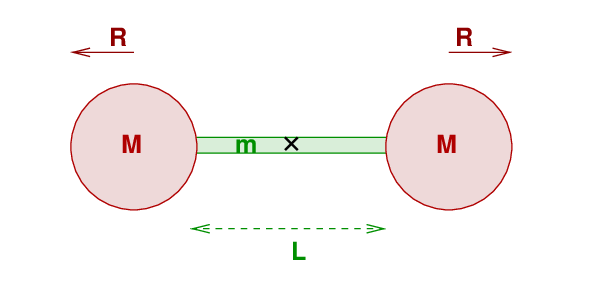
We rotate the object around its geometric center, marked with an "X" in the figure above.
Q: What is the moment of inertia of each ball around its own center?
Q: What is the distance from the center of each ball to
the axis of rotation?
Q: What is the moment of inertia of each ball around the center?
Q: What is the moment of inertia of the rod?
Q: What is the moment of inertia of the entire object?
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.