 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
If all other methods fail, we can find the moment of inertia of any object around any axis of rotation by performing an integral. The basic idea goes back to the simplest definition of moment of inertia: for a set of discrete point masses,
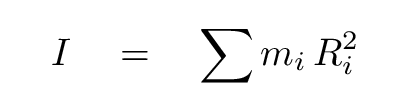
We can do the same thing for a continuous object, as long as we break it up into really small, teeny-tiny pieces. Lots and lots of teeny-tiny pieces. If
the mass of each little piece is dm the distance of each piece from axis of rotation is R
then the moment of inertia is the integral of the mass of each little piece, times its distance from axis squared:
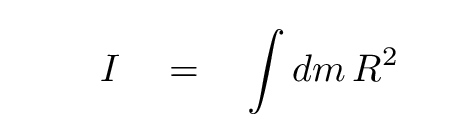
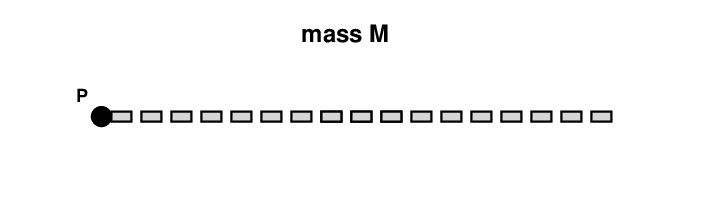
Consider a long, thin rod, with mass M and length L. That means that the linear mass density is λ = (M/L) kg/meter.
The rod is pinned to the wall at point P, so that it can swing around that position.
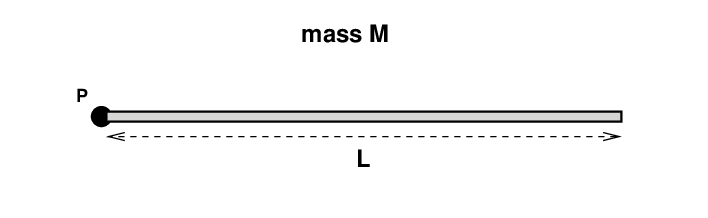
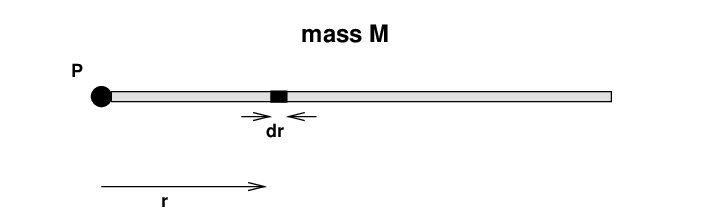
The method we'll use is to break up the rod into a bunch of tiny little pieces. We can compute the mass of each teeny piece, and its teeny moment of inertia around point P ... and then add up all those little moments of inertia.
The steps in the process are:
 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.