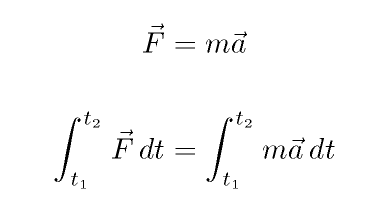
 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
So far, we've applied two sets of tools to understand what happens when objects interact:
But there are some very common, very important situations in which we need a new tool -- momentum.
Let's look at things in a bit of detail ..
You know some equations which connect changes in velocity to forces and accelerations .... but that isn't the complete story. Do your kinematic equations help you to answer this question:
I'm driving a car at 55 mph along the highway. How big a force will it take to stop me and my car?
The answer is -- it depends.
Your kinematic equations assume that the force is constant in size; what if it isn't? We can still use Newton's Second Law to say something about the behavior of the object under a time-variable force:
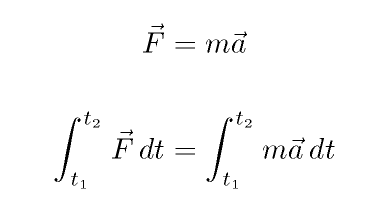
As long as the mass of the object(s) doesn't change, then we can take the m out of the integral:
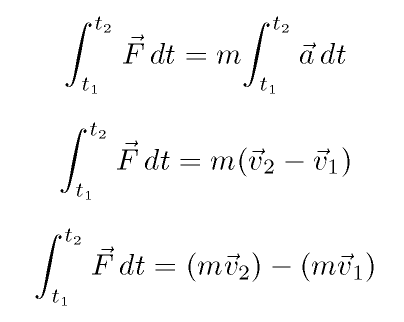
And now, if we define momentum p as the product of mass and velocity, we have
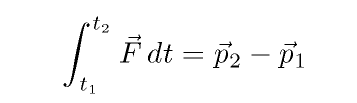
In words, we can say that
the change of a body's momentum is equal to the integral of the forces on it over time
Some guy named Newton wrote something along these lines:

Physicists have given the name impulse to the quantity "force integrated over time".
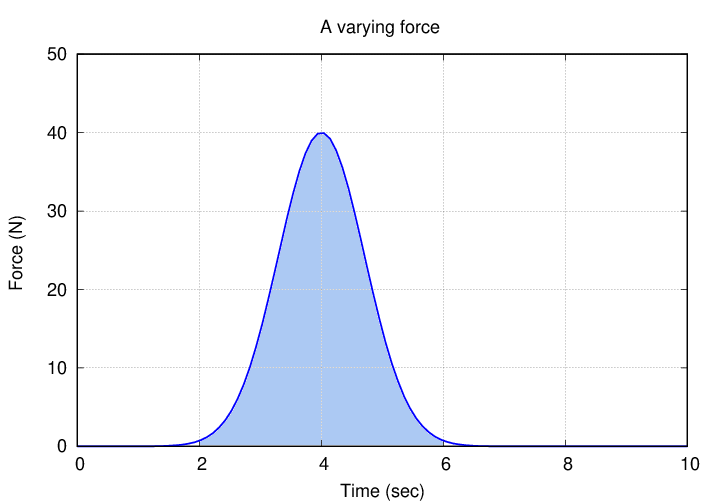
Q: What is the impulse due to the force above?
(A rough estimate is fine)
In the special case that a force is constant, the impulse it imparts is simply "force multiplied by time."
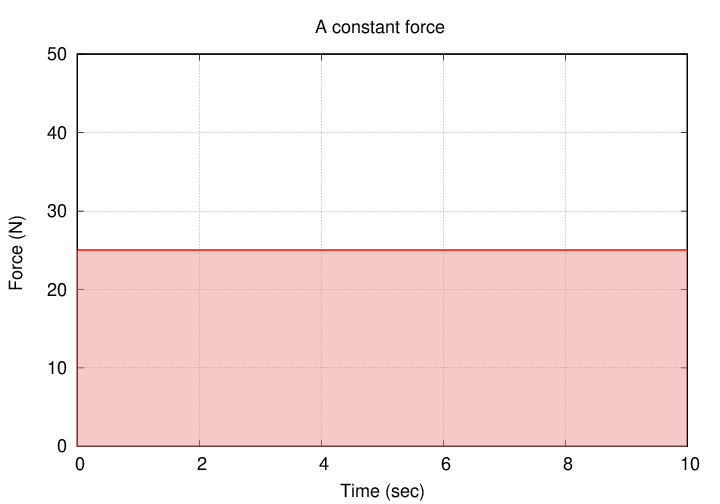
Q: Is the impulse due to this constant force greater or smaller
that that due to the varying force?
Today you will use impulse to solve some problems.
Momentum turns out to be enormously useful in solving problems which involve collisions, even when you don't know the details. Why? Because under very common circumstances, the total momentum of a set of colliding objects will be the same before and after they collide; in other words, momentum is conserved.
To be rigorous, we can only apply the conversation of momentum to a "closed system"; in other words, a system which is not affected by external forces. But if we zoom in to concentrate on just one small span of time, we can achieve decent results in many cases.
As long as there are no net external forces, momentum will always be conserved in any collision. That makes momentum a very powerful tool for dealing with collisions. Kinetic energy, on the other hand, is not always conserved in collisions. Given the choice, then, it's usually better to try using momentum, rather than kinetic energy, if you face a complicated collision between several objects.
 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.