The potential energy of a spring

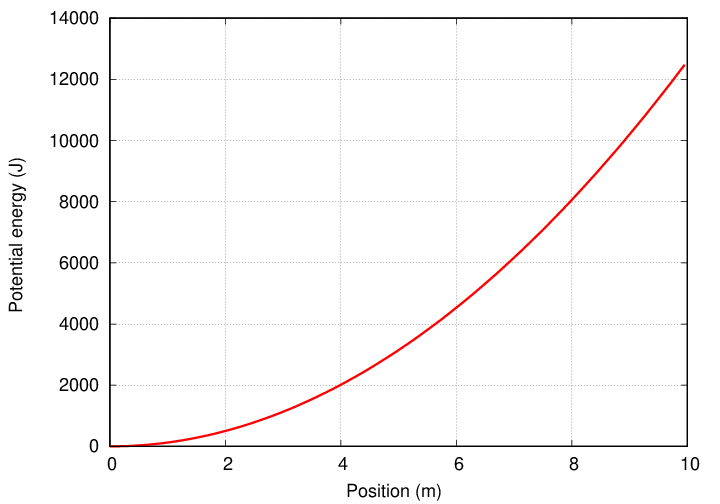
Marcy finds an old spring by the side of the railroad tracks -- maybe it fell off a train. She takes it home and performs a few experiments, stretching it by various distances and measuring the potential energy of the spring at each position. She makes a graph showing the results: the potential enerby of the spring as a function of the distance it has stretched.

"Hmmm," thinks Marcy, "that looks like a quadratic relationship." A bit of algebra shows that it is.

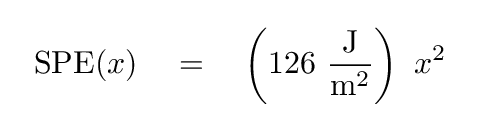
"Potential energy is okay," muses Marcy, "but what I'd really like to know is the force exerted by this spring at some distance. Like, say, when it has stretched by 5 meters."



  Q:  How can Marcy compute the force exerted by her spring
             when it has stretched by 5 meters?

All she has to do is take the derivative of the potential energy function with respect to position x. Oh, and she must remember that minus sign, too.



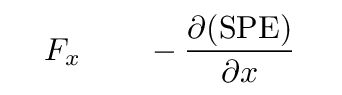
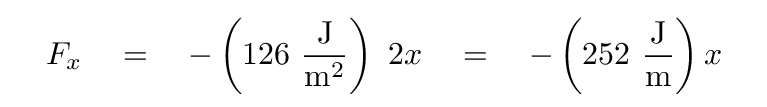
   Q:  What is the force exerted by the spring at a stretch
             of 5 meters?

My answer.

Marcy could also use her graph of potential energy as a function of position to find the force. All she needs to do is measure the slope of the curve at the desired position ... and then multiply by negative one.

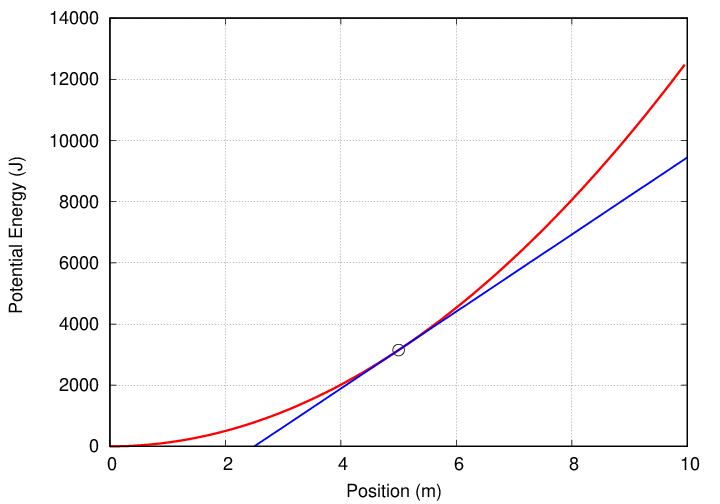
A rough reading of the graph yields a slope of



                      rise          (9500 - 0) J
       slope   =   ----------  ≈   --------------  =  1266 N
                      run           (10 - 2.5) m

and thus we could estimate that the force is F ≈ -1266 N.