Potential energy and escape velocity

Using energy is an efficient way to solve many real-world physics problems. For example, how fast would we have to fire a cannonball in order to make it fly away from the Earth forever? In other words, what is the escape velocity of the Earth?

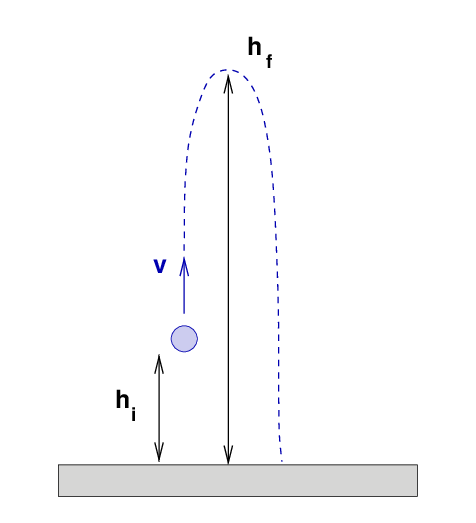
Let's start with a simple example -- one which is TOO simple to help. Fred throws a ball vertically upward. The ball leaves his hand at a height h_i = 1 m, with a speed v = 10 m/s.



  Q:  What is the maximum height of the ball's trajectory?

One could use 1-D kinematics to solve this problem, because the acceleration due to gravity is constant as the ball flies through the air. Or, one could use energy. Let's use the second method. The first step is to write down all the forms of energy which are involved in the problem ...

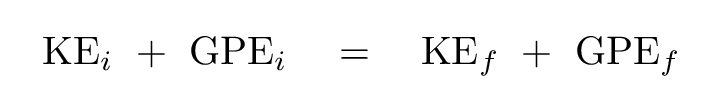
... and then we insert the appropriate expressions for kinetic and gravitational potential energy.

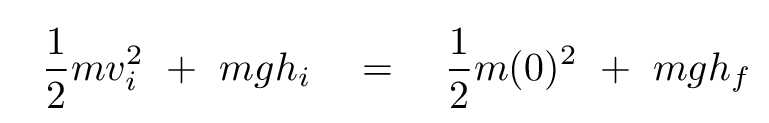
Then we can plug in the numbers and solve for the final height, finding h_f = 6.1 m above the ground.

That first example was a little too simple: because the ball was always so close to the Earth's surface, the gravitational force on it was a constant size, m*g. But if we fire a ball upward at very high speed, it will move so far far from the Earth that the gravitational force begins to decrease.

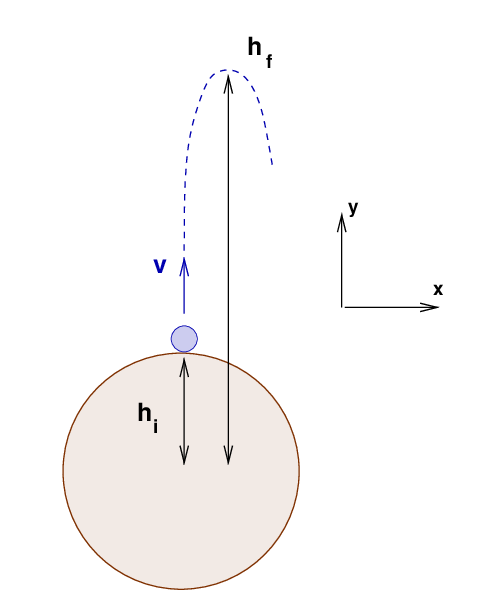
That means that we need to use the universal law of gravitation in order to compute the change in gravitational potential energy as the ball flies away from the Earth. That means that we CANNOT use 1-D kinematics any more. We must use energy.

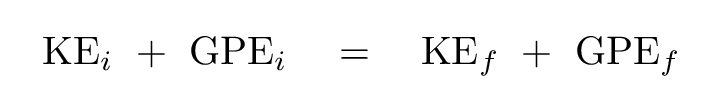
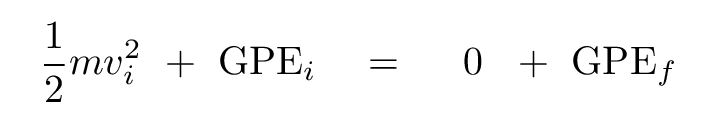
That change in gravitational potential energy now involves an integral.



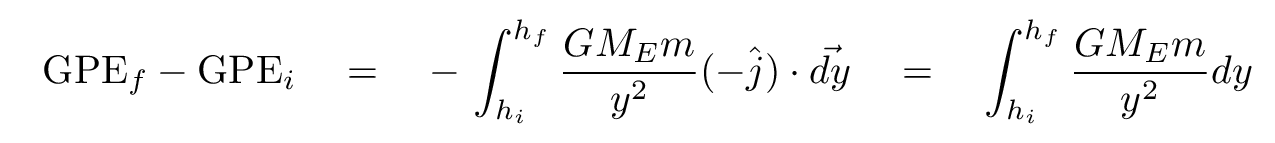
  Q:  Can you perform this integration?

It's not so bad:

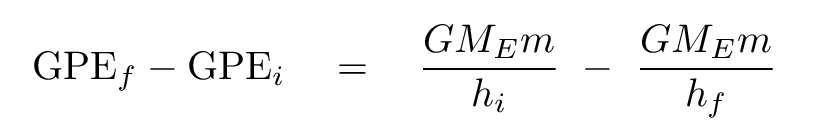
We can now re-arrange the terms in our equation for the conservation of energy so that they look like

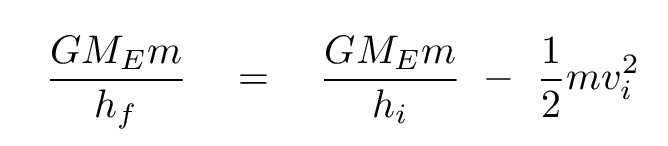
which finally leads to an equation for the height this ball will reach:



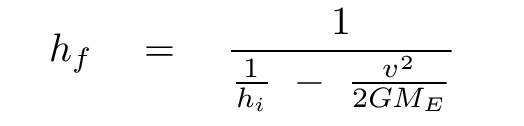
  Q:  Suppose that we fire a ball vertically upward from the Earth's
           surface with a speed of v_i = 3000 m/s.  How far up will it go?

My answer

Sending a projectile to infinity -- escape velocity

But what if I want to send the ball to a final distance of INFINITY? In other words, what how fast must I fire the ball upward so that it NEVER comes back?

It's easy to find this escape velocity if one uses the energy approach. We start in the usual way.

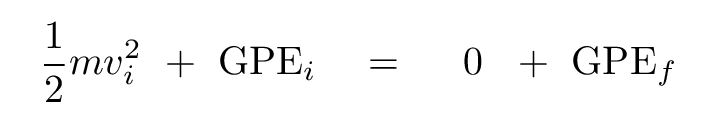
Now, the change in gravitational potential energy simplifies when the ball ends up at an infinite distance:

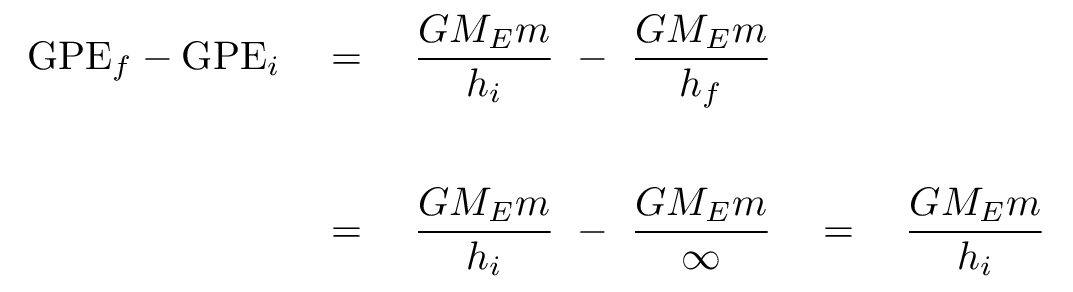
And so we end up with a nice result for the escape speed from the Earth.

Or, in general, a formula which provides the escape speed from a spherical body of mass M and radius R.



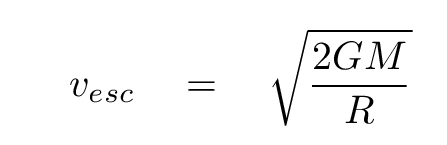
  Q:  What is the escape velocity from the Earth's surface?

My answer

How to make a black hole

Suppose that an object had a larger mass, or a smaller radius, than the Earth. Then its escape velocity would be larger than 11 km/s.

Could it be a LOT larger? Could it be ... as fast as the speed of light?



  Q:   How small would the Earth have to be in order for its
                escape velocity to equal the speed of light?

Re-arranging to solve for the critical radius, we find

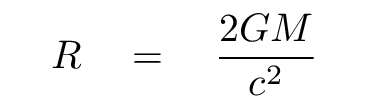
and plugging in the mass of the Earth, we find a radius of just a bit less than 1 cm! That's one compact object.

Astronomers have a special name for objects whose escape velocity is faster than the speed of light: black holes. We have detected a number of them over the past few decades:

some are the result of the collapse of a single star, ending up with masses around 10 times that of our Sun, and radii of about 30 km
some are found at the centers of galaxies, and consist of gigantic accumulations of matter, up to 1 billion times the mass of our Sun, with radii roughly as big as our Solar System

In the past year, radio astronomers combined the information gathered by a number of telescopes around the world to create an image showing hot gas swirling around one of these supermassive black holes:

Image of the gas at the center of M87 courtesy of Event Horizon Telescope Collaboration

Want to know more about this picture?

A short explanation of this "picture" of a black hole