Using the potential to determine the DIRECTION of an associated force

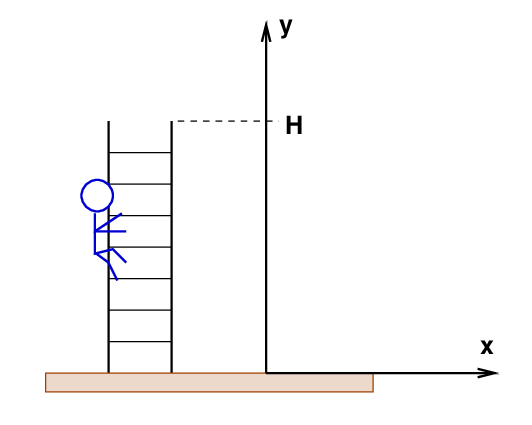
Let's take a second look at Joe as he climbs the ladder to the roof of his house. Recall that Joe's mass is m and his roof is a height H above the ground.

We know that the gravitational potential energy (GPE) of Joe when he is at a vertical distance y above the ground can be written as

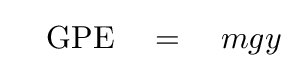
As we've discussed earlier, one can determine the force associated with a potential energy by taking the derivative with respect to position. For example, if we wish to know the force associated with this potential in the vertical direction, we take the derivative with respect to y.

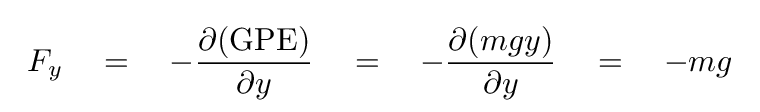
But what if we pick a different direction? Suppose that Joe reaches the roof. He can now move in a horizontal direction, too. If Joe tries to take a step to the East (positive x direction), will gravity oppose him?



   Q:  How can we determine the horizontal (x) component 
            of the gravitational force on Joe?

We can find out by taking the derivative of GPE with respect to the horizonal position x.

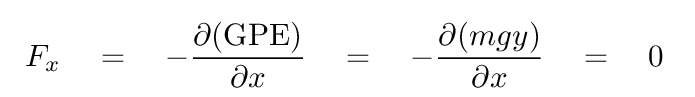
Well, that is no surprise. The gravitational force acts only in the vertical, or y, direction. If one looks at the formula for GPE, it's obvious that there won't be any force exerted in the x direction. Or the z direction, for that matter.

As a general rule, one can determine the component of a force in some particular direction by taking the derivative of the associated potential energy with respect to that direction.

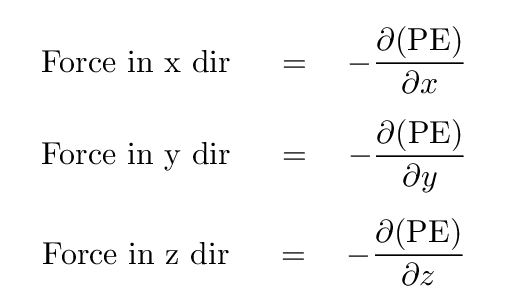
Let's look at a completely different example: the electric potential energy surrounding two small objects on a tabletop. This is an example of a contour map. You may be more familiar with their use in hiking and orienteering.

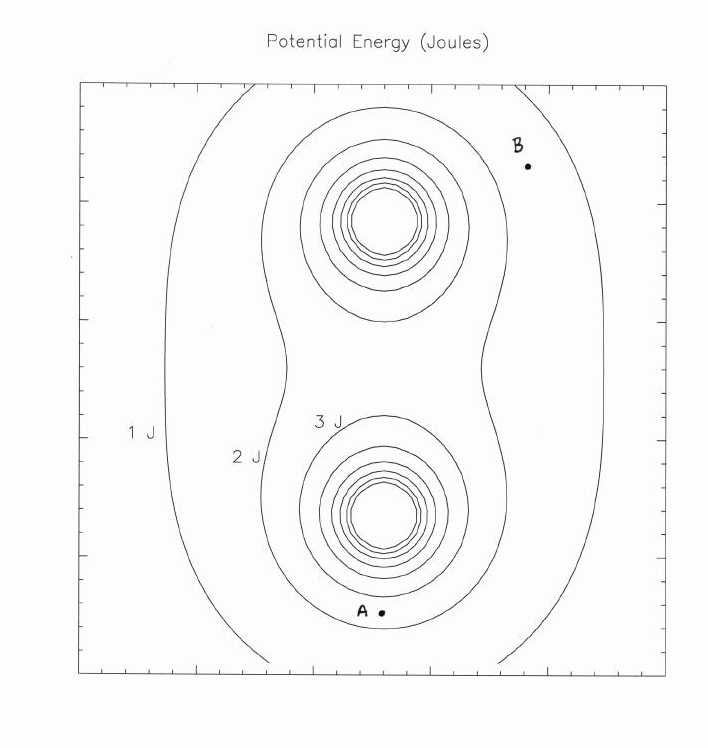
Each contour shows locations at which the electric potential energy has some particular value: 1 Joule, 2 Joules, and so forth.


  
  Q:  If one starts at point A, and moves North, how quickly does
              the potential energy change?

 
  Q:  If one starts at point A, and moves East, how quickly does
              the potential energy change?


  Q:  What can one conclude about the components of the electric FORCE
              at point A?