Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Let's walk through the process of solving a problem using energy to see how it works in detail.
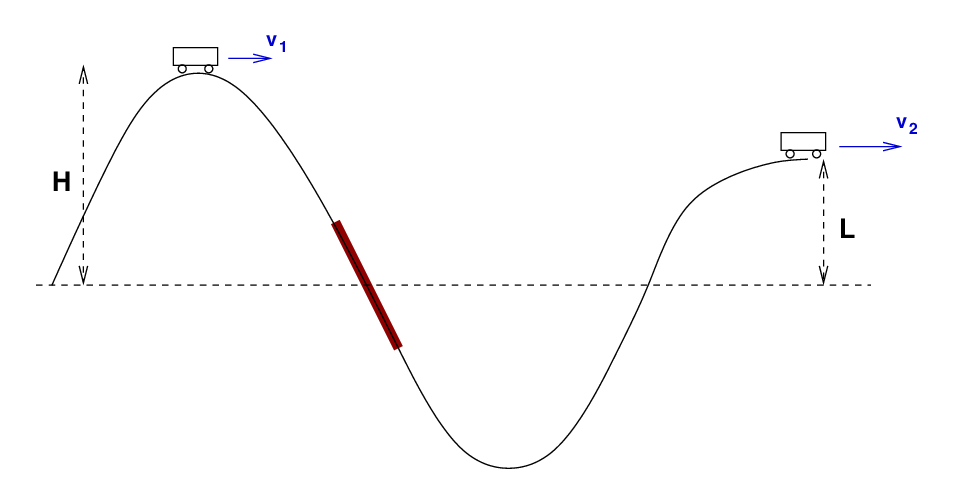
A roller-coaster cart of mass m = 200 kg rolls on a track. At the top of a hill of height H = 20 m, the cart is moving at v = 6 m/s. When the cart reaches the top of a second hill, of height L = 12 m, how fast is it going?
Q: Assuming there is no friction on the track, can you fill in
all the pieces of this equation?
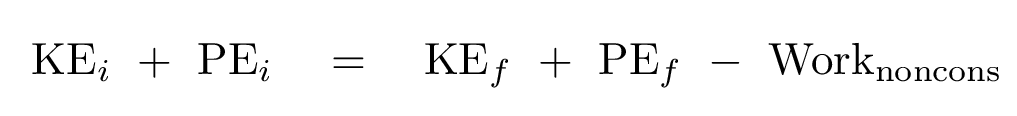
You should end up with
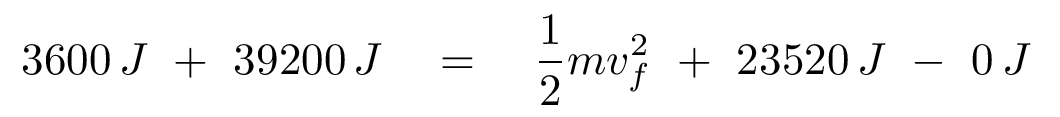
At this point, you can solve for the final speed of the cart.
Q: What is the final speed of the cart?
But what if there IS friction as the cart moves? Suppose that one section of the track of length L = 15 m, shown in red below and tilted at θ = 75 degrees, is rusty, so that the coefficient of kinetic friction between the cart and the track is μk = 0.15.
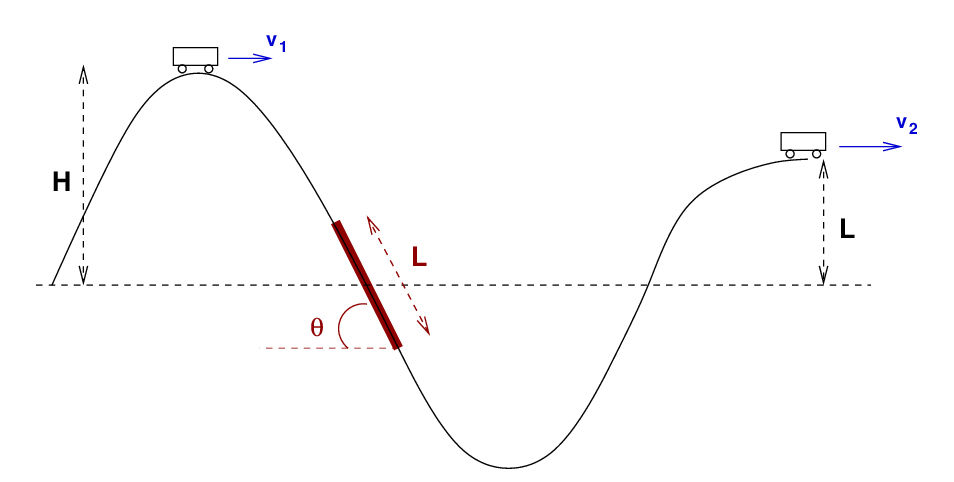
Well, we can still use energy to solve this problem, as long as we can compute the amount of work done by friction and include it properly in our equation for the conservation of energy.
How do we compute the work done by friction? Well, first we figure out the size of the friction force ...
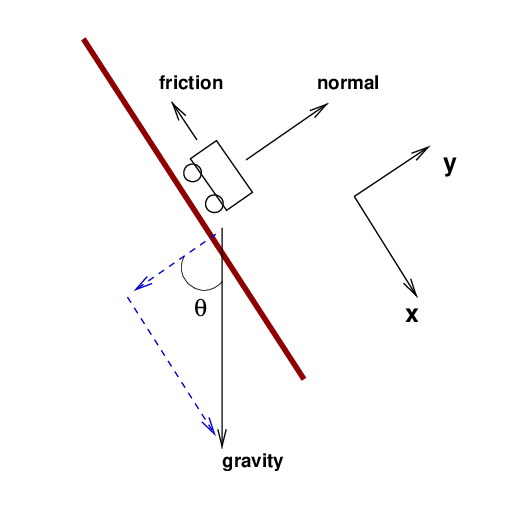
Q: What is the size of the friction force between cart and track?
Right. The force of friction has a magnitude
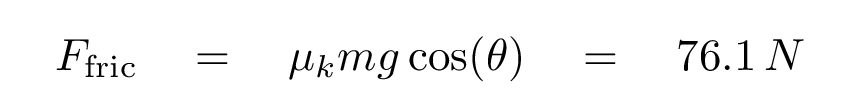
Next, we compute the amount of work done by friction as the cart rolls down this rusty section of track.
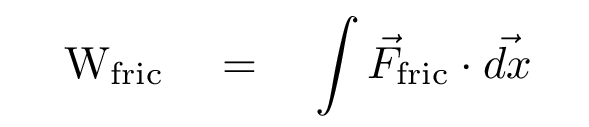
Q: What is the work done by friction?
In this case, the force of friction is always exactly opposite to the motion, so the dot product is just the size of the force, times the size of the displacement, times negative one. We end up with W(fric) = -1141.4 J .
And now it's just a matter of putting this work done by non-conservative forces back into the equation of conservation of energy.
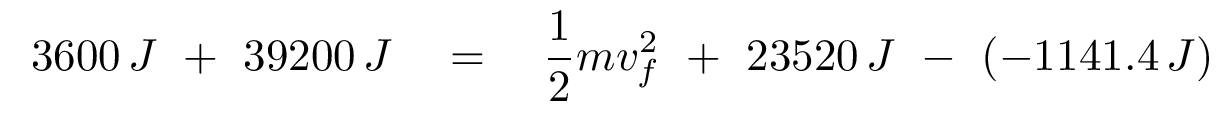
Q: So, in this case, how fast is the cart moving when it reaches
the top of the second hill?
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.