 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
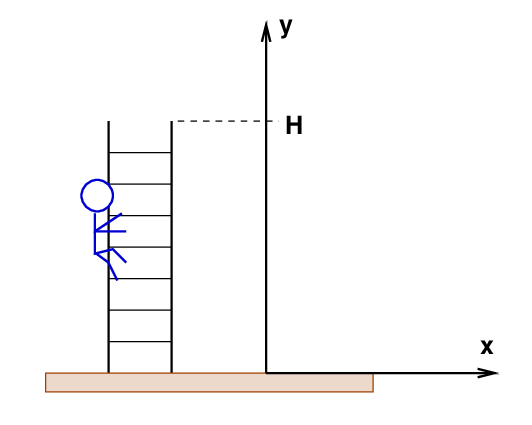
Joe (mass m) is painting his house. He starts climbing a ladder toward the roof of his house, which is a height H above the ground.

As he moves up the ladder, gravity pulls down on him.
Q: How much work does gravity do on Joe as he climbs
to the roof?
One way to compute the work done by gravity is to integrate the force over his motion. Gravity pulls down, but every little step he takes moves up.
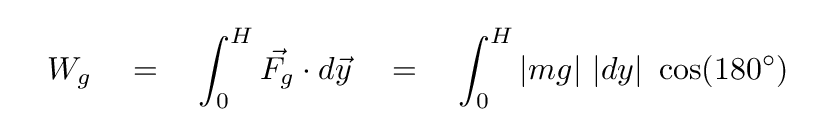
The result is that the work done by gravity is NEGATIVE.

Another way to compute the work done by gravity is to draw a graph of the force exerted by gravity as a function of Joe's position. The "area under the curve" is equal to the work done by the force.
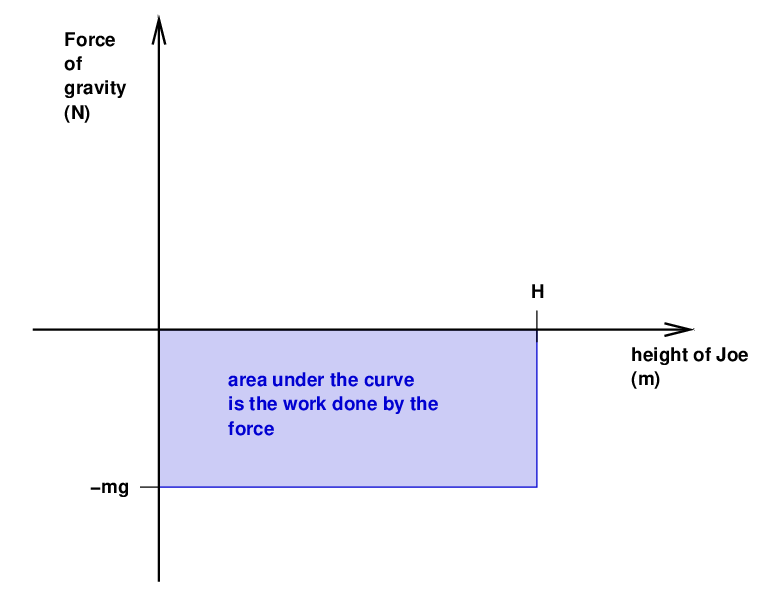
In short,
Let's watch again as Joe goes up the ladder.

This time, let's consider the change in Joe's potential energy.
Q: What is the change in Joe's gravitational potential energy (GPE)
as he climbs from the ground to the roof?
That's easy: his GPE increases by mgH.
That looks familiar. The change in GPE looks very much like the work done by gravity: Wg = -mgH. But it's not exactly the same; the work has a minus sign. In fact, the change in an object's GPE will always be equal to the negative of the work done by gravity.

This suggests that we can go backwards -- starting with potential energy and ending up with a force.
The gravitational potential energy of an object of mass m at a height y above the ground is
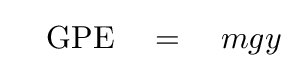
To find the force in the y-direction associated with this potential energy, we take the derivative with respect to y ... and multiply by -1:
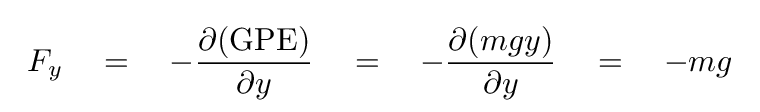
 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.