Fred on the Ferris Wheel

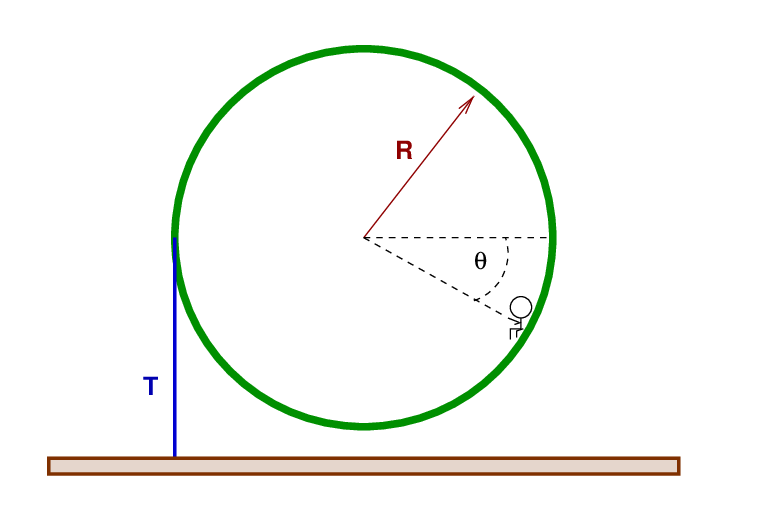
Fred goes to an abandoned amusement park and sits alone on the Ferris Wheel.

The wheel has radius R = 15 m and mass M = 6000 kg. Fred, whose mass is m = 60 kg, sits in a chair which is located θ = 30 degrees below the horizontal.

A safety cable attached to the left-hand side of the wheel prevents it from rotating. The wheel is currently motionless, and Fred sits quietly, pondering his insignificance in the universe.



  Q:  What is the size of the tension T in the cable?

Suddenly, the safety cable snaps! The wheel is free to rotate!



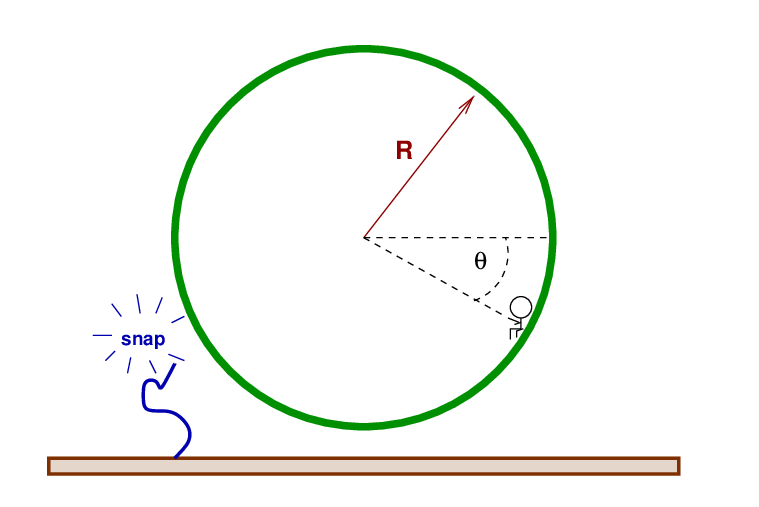
  Q:  What is the initial angular acceleration of the wheel?
          (provide magnitude, units, and direction)



  Q:  If the wheel continued to accelerate at this rate,
          how long would it take for Fred to rotate to the bottom?

But the wheel does NOT rotate with a constant angular acceleration. The torque due to Fred's weight changes as his chair moves down toward the bottom of the wheel.



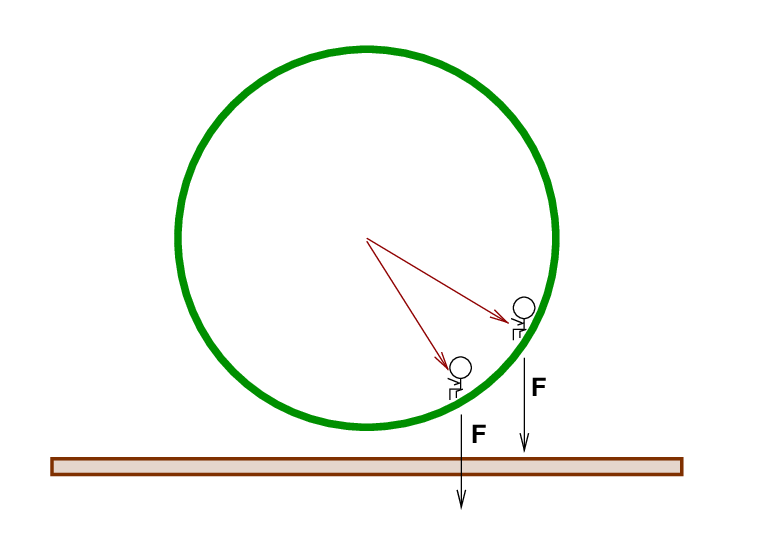
  Q:  How will the actual time for Fred's chair to rotate to the
          bottom of the wheel compare to the value we calculated earlier?


             a) it will take less time to reach the bottom of the wheel

             b) it will take more time to reach the bottom of the wheel

Because the angle between the radius and force vectors is DECREASING, the torque is also DECREASING.

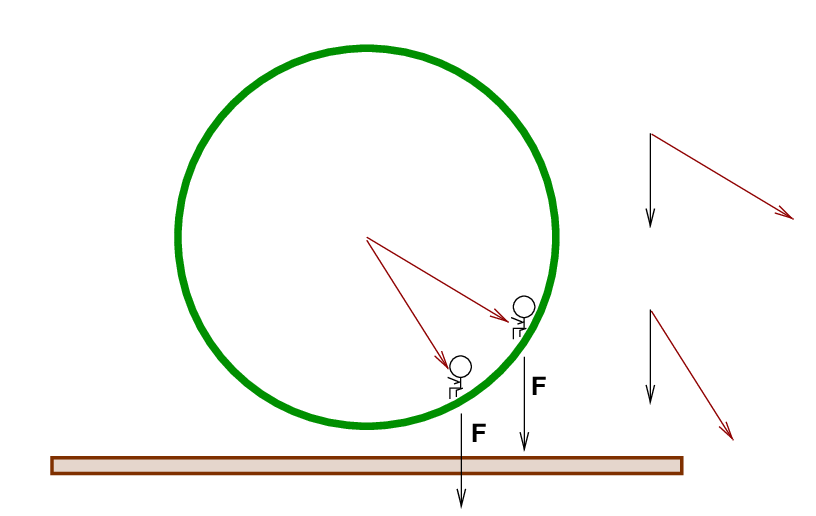
This means that the angular acceleration is constantly changing. Ugh.

We know how to calculate the motion of an object which undergoes a constant angular acceleration (or linear acceleration), but how in the world could we find a mathematical technique to predict the motion of an object which experiences a constantly changing angular (or linear) acceleration?