Using angular momentum in a "collision"

When two (or more) objects interact with each other, their total angular momentum around any point will be constant ... as long as there are no external torques acting on the objects. Let's see how this works in action.

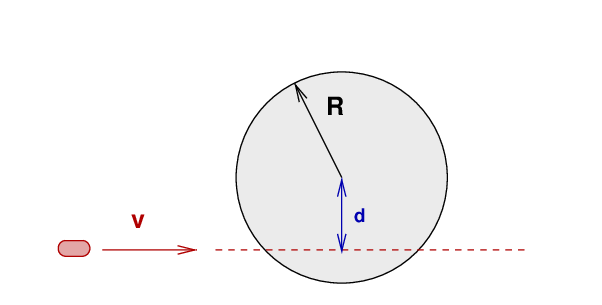
We start with two objects: a wheel sitting motionless on a rotating base, and a small barbell being carried past the wheel. This is the view from above.

Some properties of these objects we'll need to use are

barbell mass m
wheel radius R
barbell speed v
distance from center of wheel d
wheel mass M

Based on this information, can you answer these questions?


  1.  What is the moment of inertia of the wheel around its center?


  2.  What is the angular momentum of the wheel around its center 
          right now?


  3.  What is the angular momentum of the barbell around the center 
          of the wheel right now?


  4.  What is the total angular momentum around the center of the
          wheel right now?

  
  5.  What is the total kinetic energy of the objects right now?

My answers

Now, as I walk past the wheel, I gently drop the barbell so that it falls onto the wheel, at a distance d from the center of the wheel. The barbell sticks to the wheel, and the two objects start to rotate together.


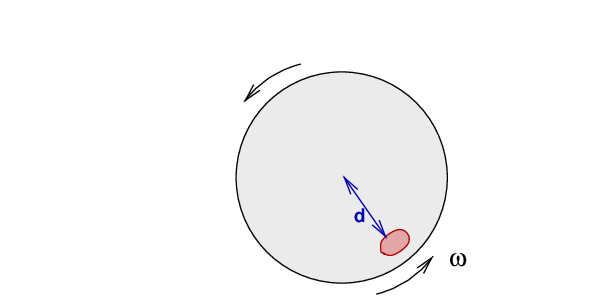
  6.  What is the angular momentum of the wheel around its center 
          right now?


  7.  What is the angular momentum of the barbell around the center 
          of the wheel right now?


  8.  What is the total angular momentum around the center of the
          wheel right now?

  
  9.  What is the total kinetic energy of the objects right now?

My answers

In class, we'll measure the properties of each object, the linear speed v of the barbell as it approaches the wheel, and the angular speed ω after the barbell has been dropped onto it.

Using these measurements, and the formulae you've written above, compute some numerical values; don't forget the units, or the directions (as needed).



 10.  What is the initial angular momentum around the center of the wheel?

 11.  What is the initial kinetic energy?

 12.  What is the total moment of inertia of the (wheel + barbell)?

Now that you know the total moment of inertia of the (wheel + barbell) as they rotate together, you can compute the final kinetic energy of the objects.



 13.  What is the final kinetic energy of the objects?

 14.  Was kinetic energy conserved during this interaction?

One final challenge for you:



 15.  Can you deduce the mass of the wheel?